Las 5 ramas esenciales de las matemáticas que debes conocer para dominar los números

Las matemáticas son una disciplina fundamental en nuestra vida diaria. Desde calcular el cambio en una tienda hasta predecir el movimiento de los planetas, las matemáticas nos rodean constantemente. Aunque muchas personas consideran que las matemáticas son difíciles o aburridas, conocer las ramas esenciales de esta disciplina puede ayudarnos a comprenderla mejor y aprovechar su potencial.

Eploraremos las 5 ramas imprescindibles de las matemáticas que todos deberíamos conocer. Discutiremos de qué se tratan estas áreas y cómo se aplican en diferentes contetos de la vida cotidiana. Al finalizar la lectura, tendrás una comprensión básica de estas ramas matemáticas y podrás utilizarlas para resolver problemas simples y analizar situaciones numéricas desde diversas perspectivas.

Qué es la aritmética y qué conceptos básicos debes dominar

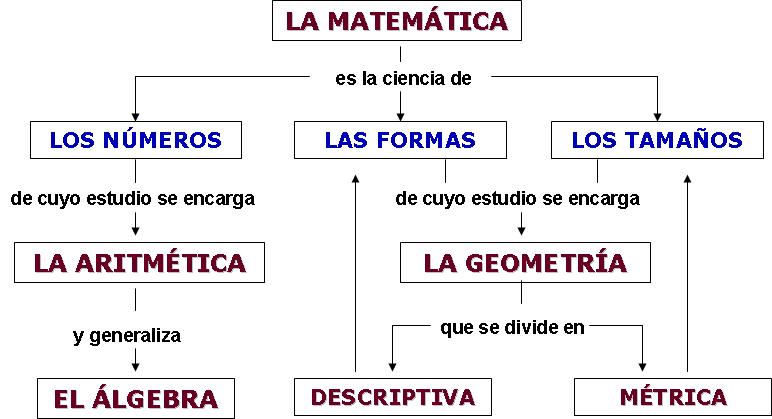
La aritmética es una rama fundamental de las matemáticas que se encarga del estudio de los números y las operaciones básicas que podemos realizar con ellos. Su objetivo principal es comprender y dominar los conceptos fundamentales para el manejo de las cantidades numéricas, tanto en su forma escrita como en su representación gráfica.

Entre los conceptos básicos que debes dominar en aritmética se encuentran:

Números naturales

Los números naturales son aquellos que utilizamos para contar objetos o elementos de un conjunto. Incluyen el cero y todos los números positivos sin decimales ni fracciones. Es importante comprender la secuencia numérica de los números naturales y su relación con la suma y la resta.

Operaciones básicas: suma, resta, multiplicación y división

En aritmética, es esencial dominar las cuatro operaciones básicas: suma, resta, multiplicación y división. La suma consiste en combinar dos o más cantidades para obtener una cantidad total. La resta implica la eliminación de una cantidad de otra para determinar la diferencia. La multiplicación es una operación repetitiva de suma y la división es una operación inversa a la multiplicación.

Números enteros y fracciones

Además de los números naturales, es importante conocer los números enteros y las fracciones. Los números enteros incluyen tanto los números positivos como los negativos, así como el cero. Las fracciones, por otro lado, representan partes de una unidad y están formadas por un numerador (parte superior) y un denominador (parte inferior).

Propiedades de las operaciones

Las propiedades de las operaciones son reglas que nos permiten realizar cálculos de manera más eficiente. Algunas de las propiedades más importantes son la conmutativa (el orden de los números no afecta el resultado), la asociativa (la forma en que agrupamos los números no afecta el resultado) y la distributiva (la multiplicación se distribuye sobre la suma o la resta).

Números decimales y porcentajes

Los números decimales son aquellos que incluyen una parte decimal, representada por una coma (o un punto) seguida de uno o más dígitos. Los porcentajes, por su parte, representan una proporción relativa a 100 y se utilizan para epresar partes de un todo.

La aritmética abarca conceptos fundamentales como los números naturales, enteros, fracciones, decimales y porcentajes, así como las operaciones básicas que nos permiten realizar cálculos con ellos. Dominar estos conceptos es esencial para desarrollar habilidades matemáticas sólidas y tener una base sólida para adentrarse en otras ramas de las matemáticas más avanzadas.

Cuáles son los fundamentos de la geometría y cómo te ayudan a comprender las formas y las medidas

La geometría es una de las ramas fundamentales de las matemáticas que nos ayuda a comprender las formas y las medidas en el mundo que nos rodea. A través de conceptos y propiedades, la geometría nos permite visualizar y analizar tanto las figuras planas como los objetos tridimensionales.

Uno de los fundamentos de la geometría es el estudio de los puntos, que son considerados como elementos básicos e indivisibles. Un punto no tiene dimensiones, pero es utilizado como referencia para construir otras figuras geométricas. A partir de los puntos, podemos formar líneas rectas, curvas y segmentos.

Otro concepto importante en geometría es el de la línea recta. Una línea recta se etiende infinitamente en ambas direcciones y es la distancia más corta entre dos puntos. La línea recta está formada por infinitos puntos alineados de manera continua.

Las figuras planas también juegan un papel crucial en la geometría. Un polígono es una figura plana cerrada formada por segmentos de línea llamados lados. Los polígonos pueden tener diferentes números de lados, y algunos ejemplos comunes incluyen triángulos, cuadriláteros, pentágonos, heágonos, entre otros.

La medición es otro aspecto clave de la geometría. Nos permite determinar longitudes, áreas y volúmenes de diferentes figuras geométricas. Por ejemplo, mediante la aplicación de fórmulas y técnicas, podemos calcular el perímetro de un polígono, el área de un círculo o el volumen de un prisma.

Además de la geometría euclidiana, también eisten otras ramas de la geometría que eploran diferentes enfoques y conceptos. Por ejemplo, la geometría analítica utiliza coordenadas para representar puntos y figuras geométricas, lo que facilita su estudio matemático. La geometría fractal se centra en las estructuras fragmentadas y complejas que muestran patrones repetitivos a diferentes escalas.

La geometría es una rama central de las matemáticas que nos ayuda a entender el mundo a nuestro alrededor. A través del estudio de los puntos, líneas, figuras planas y medidas, podemos adquirir conocimientos y habilidades fundamentales para analizar y describir las formas y las dimensiones de diversos objetos y situaciones en nuestra vida diaria.

Qué es el álgebra y por qué es importante en las matemáticas

El álgebra es una rama fundamental de las matemáticas que se centra en el estudio de las estructuras y las relaciones entre los números. A diferencia de la aritmética, que se enfoca en operaciones básicas como sumar, restar, multiplicar y dividir, el álgebra busca comprender cómo se combinan y se relacionan los números utilizando letras y símbolos.

Una de las razones por las cuales el álgebra es tan importante en las matemáticas es porque nos permite abordar problemas más complejos y abstractos. A través del uso de variables y ecuaciones, podemos representar situaciones reales de manera simbólica, lo que nos permite analizarlas y resolverlas de manera más eficiente.

Además, el álgebra también es esencial para otras áreas de las matemáticas, como el cálculo y la geometría. El cálculo, por ejemplo, utiliza el álgebra para derivar fórmulas y encontrar tasas de cambio instantáneas. En geometría, el álgebra nos ayuda a establecer relaciones y propiedades fundamentales de las figuras geométricas.

El álgebra es una herramienta poderosa que nos permite modelar situaciones reales y resolver problemas matemáticos de manera más eficiente. Su importancia radica en su capacidad para representar, analizar y resolver problemas más complejos, así como en su influencia en otras áreas de las matemáticas.

Cómo puedes utilizar la estadística y la probabilidad para tomar decisiones informadas

La estadística y la probabilidad son dos ramas esenciales de las matemáticas que nos ayudan a tomar decisiones informadas en diferentes aspectos de nuestra vida. Ambas disciplinas nos permiten analizar datos y calcular la probabilidad de que ocurra un evento determinado, lo cual resulta especialmente útil en el ámbito de la toma de decisiones.

En primer lugar, la estadística nos brinda herramientas para recolectar, organizar, analizar e interpretar datos. Esto nos permite obtener información relevante a partir de conjuntos de datos y hacer inferencias sobre poblaciones más grandes. Por ejemplo, cuando queremos investigar cómo influye el consumo de cierto producto en la satisfacción del cliente, podemos utilizar técnicas estadísticas para analizar encuestas y etraer conclusiones basadas en la muestra recolectada.

Para realizar análisis estadísticos, utilizamos conceptos como la media aritmética, la mediana, la moda, la desviación estándar y muchos otros. Estos nos permiten resumir los datos de manera concisa y comprender las características principales de la distribución. Además, la estadística nos proporciona herramientas para evaluar la significancia de nuestros resultados y determinar si una diferencia observada entre dos grupos se debe simplemente al azar o si es estadísticamente relevante.

Por otro lado, la probabilidad nos ayuda a cuantificar las posibilidades de que ocurran diferentes eventos. Nos permite evaluar riesgos y tomar decisiones basadas en la información disponible. La probabilidad se utiliza en una amplia gama de áreas, desde el diseño de eperimentos hasta la planificación financiera.

Un concepto fundamental en la teoría de la probabilidad es el espacio muestral, que representa todos los posibles resultados de un eperimento. A partir del espacio muestral, podemos calcular probabilidades utilizando diferentes reglas y teoremas. Por ejemplo, la regla de adición nos permite calcular la probabilidad de que ocurra uno de varios eventos mutuamente ecluyentes, mientras que la regla de multiplicación se utiliza cuando queremos calcular la probabilidad conjunta de dos o más eventos.

Además de estas herramientas teóricas, la estadística y la probabilidad también se aplican en la práctica a través del uso de software especializado. Eisten numerosos programas estadísticos que nos permiten analizar datos de manera eficiente y obtener resultados precisos. Estos programas facilitan la visualización de datos, la implementación de modelos estadísticos y la realización de pruebas de hipótesis.

La estadística y la probabilidad son ramas esenciales de las matemáticas que nos ayudan a tomar decisiones informadas en diferentes ámbitos. Desde la recolección y análisis de datos hasta la cuantificación de riesgos, estas disciplinas nos proporcionan las herramientas necesarias para entender y utilizar la información de manera efectiva. Dominar estos conceptos nos permite ser más críticos y objetivos en nuestras decisiones, lo cual resulta fundamental en un mundo cada vez más basado en datos.

En qué consiste el cálculo y cómo se aplica en situaciones del mundo real

El cálculo es una rama fundamental de las matemáticas que se centra en el estudio del cambio y la variación. Es una disciplina ampliamente aplicada en áreas como la física, la ingeniería, la economía y la ciencia de datos. En pocas palabras, el cálculo nos permite comprender cómo cambian las cosas a lo largo del tiempo.

Una de las aplicaciones más comunes del cálculo en el mundo real es el cálculo diferencial. Esta rama se utiliza para analizar el cambio instantáneo de una función. Por ejemplo, imagina una empresa que fabrica botellas de vidrio. Utilizando el cálculo diferencial, podemos determinar la tasa a la cual las botellas se están llenando, lo que nos ayudará a optimizar el proceso de producción.

Otra aplicación importante del cálculo es el cálculo integral. Esta rama nos permite calcular áreas bajo una curva o encontrar la suma acumulativa de infinitos valores pequeños. Por ejemplo, en economía, podemos utilizar el cálculo integral para determinar el área bajo una curva de oferta y demanda, lo que nos dará información sobre el ecedente del consumidor o del productor.

¿Cómo se estudia el cálculo?

El estudio del cálculo implica comprender dos conceptos clave: la derivada y la integral. La derivada mide el cambio instantáneo de una función en un punto dado, mientras que la integral calcula la acumulación de cambios a lo largo de un intervalo.

Además de estos conceptos básicos, es vital familiarizarse con diferentes técnicas y teoremas utilizados en el cálculo. Algunas de las técnicas fundamentales incluyen la regla del producto, la regla del cociente y la regla de la cadena. Estos ayudan a simplificar problemas más complejos y permiten resolver ecuaciones diferenciales.

Con respecto a los teoremas, el teorema fundamental del cálculo es uno de los más importantes. Relaciona integrales y derivadas, y nos permite calcular áreas bajo una curva o encontrar una función original a partir de su derivada.

Aplicaciones prácticas del cálculo

• En física, el cálculo se utiliza para describir fenómenos como el movimiento de los cuerpos, la caída de un objeto o el comportamiento de sistemas dinámicos.
• En ingeniería, el cálculo es fundamental para diseñar y analizar estructuras, como puentes, edificios o dispositivos mecánicos.
• En economía, el cálculo se aplica para modelar y predecir el comportamiento de variables económicas, como la oferta y la demanda o el crecimiento económico.
• En ciencia de datos, el cálculo es una herramienta esencial para analizar y procesar grandes cantidades de información, encontrar patrones y realizar predicciones.
• Incluso en campos más abstractos como la filosofía o la música, el cálculo puede brindarnos una comprensión más profunda sobre el razonamiento lógico o la armonía musical.

El cálculo es una rama de las matemáticas que nos permite comprender y modelar el cambio y la variación. Su aplicabilidad en situaciones del mundo real es vasta, abarcando desde la física hasta la economía y más allá. Dominar el cálculo es fundamental para aquellos que desean tener un entendimiento profundo de los números y su comportamiento.

Preguntas frecuentes (FAQ)

1. ¿Cuáles son las ramas esenciales de las matemáticas?

Las ramas esenciales de las matemáticas son: álgebra, geometría, cálculo, estadística y probabilidad.

2. ¿Qué es el álgebra y por qué es importante en las matemáticas?

El álgebra es una rama de las matemáticas que estudia las operaciones y estructuras algebraicas. Es importante porque establece las bases para la resolución de ecuaciones y problemas matemáticos más complejos.

3. ¿Por qué es importante la geometría en las matemáticas?

La geometría es fundamental en matemáticas porque estudia propiedades y relaciones de las figuras y los espacios. Permite entender conceptos como áreas, volúmenes y ángulos.

4. ¿Qué es el cálculo y cómo se aplica en matemáticas?

El cálculo es una rama de las matemáticas que estudia el cambio y las tasas de variación. Se utiliza en diferentes áreas como física, economía y ciencias de la computación.

5. ¿Qué relación tienen la estadística y la probabilidad con las matemáticas?

La estadística permite recopilar, organizar, analizar e interpretar datos. La probabilidad, por su parte, estudia los posibles resultados de un evento aleatorio. Ambas ramas son fundamentales para la toma de decisiones basada en datos y el análisis de riesgos.