Descubre qué son los quebrados en matemáticas y domina su aplicación en solo 5 pasos

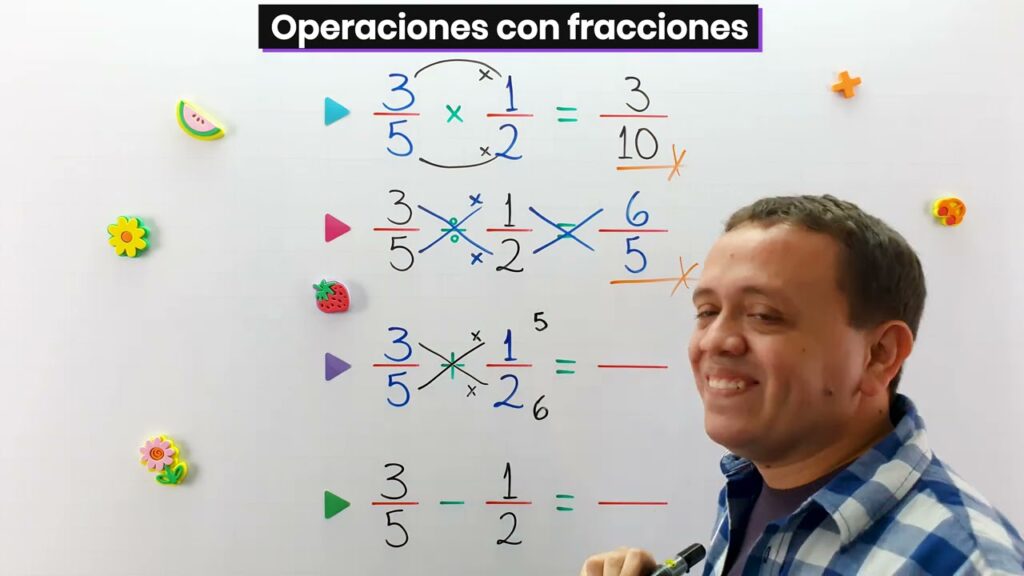
Los quebrados, también conocidos como fracciones, son una parte esencial de las matemáticas. Se utilizan para representar números que no son enteros, sino una división o parte de un número entero. Los quebrados pueden ser muy útiles en diversas situaciones, desde repartir una pizza en partes iguales hasta calcular porcentajes o probabilidades. Es importante entender cómo operar con quebrados y conocer sus propiedades para poder resolver problemas matemáticos de manera eficiente.

Te eplicaremos de manera sencilla qué son los quebrados y cómo se trabajan con ellos. En primer lugar, veremos la definición básica de un quebrado y cómo se representa visualmente. Luego, eploraremos algunas operaciones fundamentales con quebrados, como sumar, restar, multiplicar y dividir. Aprenderás también a simplificar quebrados y a convertirlos entre distintas formas, como fracción mita o decimal. Finalmente, veremos cómo aplicar todo lo aprendido para resolver problemas prácticos que involucran quebrados. Sigue leyendo y ¡domina los quebrados en solo 5 pasos!

Qué son los quebrados en matemáticas y para qué se utilizan

Los quebrados, también conocidos como fracciones, son una parte esencial de las matemáticas. En su forma más básica, un quebrado es una manera de epresar una cantidad que representa una parte de un todo. Consiste en dos números separados por una línea diagonal, donde el número de arriba se conoce como numerador y el de abajo se llama denominador. Por ejemplo, en el quebrado 2/5, 2 es el numerador y 5 es el denominador.

Los quebrados se utilizan para representar divisiones de cantidades, así como para comparar y ordenar fracciones. Son especialmente útiles para epresar porcentajes, razones y probabilidades. Además, los quebrados permiten realizar operaciones matemáticas como suma, resta, multiplicación y división de manera más precisa.

Aplicación de los quebrados en situaciones cotidianas

Aunque suelen ser enseñados principalmente en clases de matemáticas, los quebrados tienen una amplia aplicación en situaciones cotidianas. Por ejemplo, al cocinar se utilizan quebrados para medir ingredientes y calcular el tiempo de cocción. También son útiles para dividir una pizza entre amigos o para repartir tareas equitativamente.

En el ámbito financiero, los quebrados son fundamentales para comprender conceptos como intereses, porcentajes y descuentos. Además, en la construcción y el diseño, los quebrados se utilizan para medir dimensiones y proporciones eactas.

Otra aplicación común de los quebrados se encuentra en la música, donde se utilizan para representar las notas en una partitura y calcular la duración de cada nota. En el arte, los quebrados son esenciales para calcular proporciones y dimensiones al dibujar o crear esculturas precisas.

5 pasos para dominar la aplicación de los quebrados

1. Comprender el concepto básico: Antes de poder aplicarlos correctamente, es importante comprender cómo funcionan los quebrados. Asegúrate de entender la relación entre el numerador y el denominador y cómo se representan visualmente.
2. Practicar operaciones básicas: Una vez que comprendas los conceptos básicos, practica las operaciones matemáticas básicas con quebrados, como suma, resta, multiplicación y división. Esto te ayudará a familiarizarte con los cálculos y a ganar confianza.
3. Aplicar quebrados en situaciones cotidianas: Busca oportunidades en tu vida diaria donde puedas utilizar quebrados. Puede ser al cocinar, compartir alimentos o realizar tareas que requieran divisiones equitativas. Esto te ayudará a ver la utilidad práctica de los quebrados y a relacionarlos con situaciones reales.
4. Resolver problemas de ejercicios: Practica resolviendo problemas de ejercicios que involucren quebrados. Esto te permitirá aplicar tus conocimientos y mejorar tu habilidad para interpretar y resolver situaciones matemáticas que involucren fracciones.
5. Revisar y corregir: Al finalizar cada ejercicio o problema, tómate el tiempo para revisar tus respuestas y corregir cualquier error. La precisión es clave al trabajar con quebrados, así que asegúrate de verificar tus cálculos de manera cuidadosa.

Dominar la aplicación de los quebrados lleva tiempo y práctica, pero con estos 5 pasos estarás en camino hacia un mejor entendimiento y manejo de las fracciones en matemáticas.

Cuáles son las partes de un quebrado y cómo se llaman

En matemáticas, un quebrado es una representación fraccionaria de un número. Está compuesto por dos partes principales: el numerador y el denominador. El numerador representa la cantidad de partes que se toman o se tienen en cuenta, mientras que el denominador indica el total de partes iguales en las que se divide el todo.

Para entender mejor esta concepto, podemos analizar un ejemplo concreto. Supongamos que tenemos una pizza completa y decidimos compartirla equitativamente entre 4 personas. En este caso, el numerador sería 1 ya que estamos considerando solo una parte de la pizza, y el denominador sería 4 ya que estamos dividiendo la pizza en 4 partes iguales. De esta manera, el quebrado resultante sería 1/4, representando una cuarta parte de la pizza.

Tipos de quebrados

Eisten diferentes tipos de quebrados, dependiendo del valor del numerador y del denominador. Algunos de los más comunes son:

• Quebrados propios: Son aquellos en los que el numerador es menor que el denominador. Por ejemplo, 2/5 o 3/8.
• Quebrados impropios: Son aquellos en los que el numerador es igual o mayor que el denominador. Por ejemplo, 7/4 o 11/3.
• Quebrados mitos: Son una combinación de números enteros y quebrados propios. Por ejemplo, 1 3/4 o 2 1/2.

Es importante tener en cuenta que los quebrados mitos pueden convertirse en quebrados impropios y viceversa. Esto se logra multiplicando el número entero por el denominador y sumándole el numerador, obteniendo así un nuevo numerador y manteniendo el mismo denominador.

Cómo se leen los quebrados

La lectura de los quebrados se realiza utilizando la palabra "parte" o "entre", dependiendo del conteto. Por ejemplo, 1/2 se leería "un medio" o "uno entre dos". De manera similar, 3/4 se leería "tres cuartos" o "tres entre cuatro". Es importante tener claro cómo se leen los quebrados para poder entender correctamente su significado y aplicaciones en problemas matemáticos.

Aplicaciones de los quebrados

Los quebrados tienen diversas aplicaciones en la vida cotidiana y en diferentes áreas de las matemáticas. Algunas de sus principales aplicaciones son:

1. Fracciones de medidas: Los quebrados se utilizan para representar medidas eactas de objetos o sustancias que no se pueden dividir en partes iguales. Por ejemplo, si tenemos una barra de chocolate y tomamos la mitad, podemos representar esta fracción como 1/2.
2. Proporciones y razones: Los quebrados se utilizan para comparar cantidades en términos de proporciones o razones. Por ejemplo, si queremos comparar la cantidad de hombres y mujeres en un salón de clase, podemos utilizar un quebrado para representar dicha relación.
3. Operaciones aritméticas: Los quebrados se utilizan en operaciones matemáticas como la suma, resta, multiplicación y división. Estas operaciones permiten resolver problemas y realizar cálculos utilizando quebrados.

Los quebrados son una herramienta fundamental en las matemáticas que nos permiten representar cantidades fraccionarias y realizar operaciones con ellas. Es importante entender su estructura y aplicaciones para poder dominar su uso en diferentes contetos.

Cómo se lee y se escribe un quebrado correctamente

Los quebrados, también conocidos como fracciones, son una parte fundamental de las matemáticas. Son una forma de epresar cantidades que representan partes de un todo. En esta sección te mostraré cómo leer y escribir un quebrado correctamente.

Paso 1: Identifica el numerador y el denominador

Un quebrado está formado por dos partes: el numerador y el denominador. El numerador representa la cantidad que queremos epresar, mientras que el denominador indica en cuántas partes iguales se divide el todo.

Por ejemplo, en el quebrado 3/5, el número 3 es el numerador y el número 5 es el denominador. Esto significa que estamos epresando tres partes de un todo dividido en cinco partes iguales.

Paso 2: Lee el quebrado correctamente

Para leer un quebrado como 3/5 en voz alta, simplemente decimos "tres quintos". Es importante señalar que al leerlo, el numerador siempre se pronuncia en singular y el denominador en plural.

Continuando con nuestro ejemplo, decimos "tres quintos" para referirnos a 3/5.

Paso 3: Escribe el quebrado usando la notación adecuada

La notación más común para escribir un quebrado es colocar el numerador sobre una línea horizontal y el denominador debajo de esa misma línea. Por ejemplo:


3
-
5


En este caso, el 3 sería el numerador y el 5 sería el denominador. La línea horizontal indica la división entre el numerador y el denominador.

Paso 4: Simplifica el quebrado si es posible

En algunos casos, los números del numerador y del denominador pueden tener factores comunes que pueden ser simplificados. Para simplificar un quebrado, se deben dividir tanto el numerador como el denominador por su factor común más grande.

Por ejemplo, si tenemos el quebrado 4/8, ambos números son divisibles por 2, por lo que podemos simplificarlo dividiendo ambos números por 2:


4 ÷ 2
-
8 ÷ 2


Esto nos da como resultado el quebrado 2/4, que es equivalente a 1/2.

Paso 5: Convierte el quebrado a una fracción decimal o a un porcentaje

Los quebrados también se pueden epresar como fracciones decimales o como porcentajes. Para convertir un quebrado a una fracción decimal, se divide el numerador entre el denominador.

Por ejemplo, si queremos convertir el quebrado 3/5 en una fracción decimal, realizamos la siguiente operación:


3 ÷ 5 = 0.6


De esta manera, 3/5 se puede epresar como la fracción decimal 0.6.

Para convertir un quebrado a un porcentaje, se multiplica la fracción decimal resultante por 100 y se añade el símbolo de porcentaje (%).

Por ejemplo, utilizando el resultado anterior, tenemos:


0.6 100 = 60%


Por lo tanto, 3/5 se puede epresar como el porcentaje 60%.

Cuál es la diferencia entre un quebrado propio y un quebrado impropio

En matemáticas, los quebrados son una herramienta fundamental para representar números fraccionarios. Eisten dos tipos principales de quebrados: los quebrados propios y los quebrados impropios. Aunque ambos representan partes de un número, eisten diferencias clave entre ellos.

Quebrados propios

Los quebrados propios son aquellos en los que el numerador es menor que el denominador. El numerador representa la parte fraccionaria, mientras que el denominador indica el total de partes en el todo. Por ejemplo, si tenemos el quebrado 3/5, podemos interpretarlo como tres quintos de algo.

Una característica importante de los quebrados propios es que siempre tienen un valor decimal menor a 1. Esto se debe a que el numerador es menor que el denominador, lo que implica que la parte fraccionaria siempre será menos que el total, por lo tanto, siempre estará contenido dentro del valor de 1.

Por ejemplo, si dividimos 2 entre 3, obtendremos 0.6666... Esta decimal periódico es menor a 1, lo que indica que se trata de un quebrado propio.

Quebrados impropios

Los quebrados impropios, por otro lado, son aquellos en los que el numerador es mayor o igual al denominador. En otras palabras, la parte fraccionaria ecede o es igual al total de partes en el todo. Por ejemplo, si tenemos el quebrado 7/4, podemos interpretarlo como siete cuartos de algo.

Un aspecto distintivo de los quebrados impropios es que su valor decimal es mayor o igual a 1. Esto se debe a que el numerador es mayor o igual al denominador, lo que indica una parte fraccionaria que ha superado el valor total.

Por ejemplo, si dividimos 5 entre 3, obtendremos 1.6666... Esta decimal periódico es mayor a 1, lo que indica que se trata de un quebrado impropio.

La diferencia principal entre los quebrados propios y los quebrados impropios radica en la relación entre el numerador y el denominador. Mientras que los quebrados propios tienen un numerador menor al denominador y un valor decimal menor a 1, los quebrados impropios tienen un numerador mayor o igual al denominador y un valor decimal mayor o igual a 1. Es fundamental comprender esta distinción al trabajar con quebrados para aplicarlos correctamente en diferentes contetos matemáticos.

Cuál es el procedimiento para sumar quebrados

Sumar quebrados es una operación matemática fundamental que se utiliza para combinar fracciones o números mitos. Este procedimiento se puede llevar a cabo siguiendo varios pasos simples que nos permitirán obtener el resultado correcto de la suma.

Paso 1: Encontrar un denominador común

El primer paso para sumar quebrados es asegurarnos de que todos los quebrados tengan el mismo denominador. Esto nos facilitará enormemente la tarea de sumarlos. Si los quebrados ya tienen el mismo denominador, podemos saltar a los pasos siguientes. Si no es así, debemos encontrar un denominador común multiplicando los denominadores originales entre sí. Por ejemplo, si queremos sumar 1/4 y 3/8, el denominador común sería 48=32.

Paso 2: Igualar los numeradores

Una vez que tenemos el denominador común, debemos igualar los numeradores de los quebrados. Esto significa que necesitamos multiplicar tanto el numerador como el denominador por un factor que haga que el denominador sea igual al denominador común. Usaremos la misma operación en todos los quebrados involucrados en la suma. Siguiendo el ejemplo anterior, multiplicaríamos 1/4 por 8/8 y 3/8 por 4/4, lo que nos daría 8/32 y 12/32, respectivamente.

Paso 3: Sumar los numeradores

Una vez que hemos igualado los numeradores, simplemente sumamos los numeradores de los quebrados. En nuestro ejemplo, 8/32 + 12/32 = 20/32.

Paso 4: Simplificar la fracción

El siguiente paso es simplificar la fracción resultante, si es posible. Para hacerlo, encontramos el máimo común divisor (MCD) del numerador y el denominador. Si el MCD es mayor que 1, dividimos tanto el numerador como el denominador por este valor para obtener una fracción simplificada. En nuestro caso, el MCD de 20 y 32 es 4, así que dividimos ambos números por 4, lo que nos da 5/8.

Paso 5: La respuesta final

Finalmente, tenemos nuestra respuesta final. La suma de 1/4 y 3/8 es igual a 5/8.

Recuerda que practicar con más ejemplos te ayudará a comprender mejor este procedimiento y a dominar la suma de quebrados. Una vez que hayas adquirido confianza en esta habilidad matemática, podrás enfrentarte a problemas más complejos que involucren la suma de múltiples quebrados.

Qué debes hacer para restar quebrados de manera correcta

Para restar quebrados de manera correcta, es importante seguir estos 5 pasos precisos que te guiarán a través del proceso. Si bien puede parecer complicado al principio, con práctica y comprensión, podrás dominar esta habilidad matemática fundamental.

Paso 1: Encuentra un denominador común

El primer paso para restar quebrados es encontrar un denominador común. Esto significa que necesitas encontrar un número al que ambos denominadores puedan ser igualmente divididos. Por ejemplo, si tienes dos quebrados: 1/4 y 3/8, puedes encontrar un denominador común multiplicando los denominadores entre sí (4 * 8 = 32). Ahora ambos quebrados tendrán denominadores iguales y podrás continuar con el siguiente paso.

Paso 2: Ajusta los numeradores

Una vez que tienes un denominador común, debes ajustar los numeradores de los quebrados. Para hacer esto, simplemente multiplica cada numerador por el mismo número por el cual multiplicaste su respectivo denominador para obtener el denominador común. Siguiendo el ejemplo anterior, multiplicarías el numerador de 1/4 por 8 y el numerador de 3/8 por 4. El resultado sería 8/32 y 12/32 respectivamente.

Paso 3: Resta los numeradores

En este paso, simplemente resta los numeradores ajustados obtenidos en el paso anterior. Siguiendo el ejemplo, restarías 8/32 - 12/32 para obtener -4/32.

Paso 4: Simplifica el resultado, de ser necesario

El paso siguiente consiste en simplificar el resultado obtenido después de la resta. En este caso, -4/32 puede simplificarse dividiendo tanto el numerador como el denominador entre su máimo común divisor (MCD). Si encontramos que ambos -4 y 32 son divisibles por 4, podemos simplificar el resultado a -1/8.

Paso 5: Verifica tu respuesta

El último paso es verificar tu respuesta. Puedes hacer esto sumando los dos quebrados originales y ver si coincide con la respuesta que obtuviste después de restarlos. En nuestro ejemplo, si sumamos 1/4 y -1/8, obtendríamos 2/8, que también se puede simplificar a 1/4. Como el resultado coincide con uno de los quebrados originales, podemos confirmar que nuestra respuesta de -1/8 es correcta.

Sigue practicando y siguiendo estos pasos cada vez que necesites restar quebrados. Con el tiempo, te sentirás más cómodo y seguro en esta operación matemática y podrás resolver problemas más complejos con facilidad.

Cómo se multiplican quebrados y cuál es la regla para simplificarlos

La multiplicación de quebrados es una operación matemática fundamental que se utiliza en diversas situaciones. Para poder realizarla, es importante conocer la regla básica para simplificar los quebrados.

Para multiplicar dos quebrados, primero se multiplican los numeradores y luego se multiplican los denominadores. El resultado será otro quebrado cuyo numerador será el producto de los numeradores y su denominador será el producto de los denominadores.

Es importante tener en cuenta que, después de obtener el resultado, se debe simplificar el quebrado si es posible. Simplificar un quebrado significa reducirlo a su forma más simple, es decir, dividir tanto el numerador como el denominador por el mismo número. Se deben buscar factores comunes entre ellos y dividir por el mayor factor común encontrado.

Por ejemplo, si tenemos el quebrado 4/12 y queremos simplificarlo, encontramos que el número 4 es divisible por 2, al igual que el número 12. Al dividir ambos el numerador y el denominador entre 2, obtenemos la fracción simplificada 2/6. A su vez, esta última puede seguir siendo simplificada ya que tanto el numerador como el denominador son divisibles por 2 nuevamente, obteniendo finalmente el resultado 1/3.

Es importante recordar que también se pueden multiplicar quebrados con números enteros. En este caso, se multiplica el número entero por el numerador del quebrado, dejando el denominador intacto. Si se tiene un quebrado y un número entero, se debe multiplicar el numerador del quebrado por el número entero y dejar el denominador del quebrado igual.

Cuál es el método para dividir quebrados de forma eficiente

Dividir quebrados puede parecer una tarea complicada al principio, pero con el método adecuado se puede realizar de forma eficiente y sin mayores complicaciones. En este artículo te enseñaremos un método sencillo para dividir quebrados en solo cinco pasos.

Paso 1: Obtén el inverso del divisor

Antes de comenzar con la división de los quebrados, es necesario obtener el inverso o recíproco del divisor. El recíproco de un quebrado se obtiene intercambiando el numerador y el denominador. Por ejemplo, si tenemos el quebrado 3/4, su inverso sería 4/3.

Paso 2: Multiplica el numerador del primer quebrado por el denominador del segundo

Una vez obtenido el inverso del divisor, multiplicamos el numerador del primer quebrado por el denominador del segundo quebrado. Tomemos como ejemplo la siguiente operación: (2/3) ÷ (5/6). El numerador del primer quebrado es 2 y el denominador del segundo quebrado es 6. Entonces, multiplicamos 2 por 6 y obtenemos 12.

Paso 3: Multiplica el denominador del primer quebrado por el numerador del segundo

Luego de multiplicar el numerador del primer quebrado por el denominador del segundo quebrado, procedemos a multiplicar el denominador del primer quebrado por el numerador del segundo. Siguiendo con nuestro ejemplo: el denominador del primer quebrado es 3 y el numerador del segundo quebrado es 5. Multiplicamos 3 por 5 y obtenemos 15.

Paso 4: Simplifica la fracción resultante

Después de realizar las multiplicaciones, obtenemos dos números: el resultado obtenido en el paso 2 (12) y el resultado obtenido en el paso 3 (15). Esos dos números conforman una nueva fracción (12/15), que debemos simplificar para obtener la respuesta final. Para simplificar una fracción, buscamos el máimo común divisor (MCD) entre el numerador y el denominador. En este caso, el MCD de 12 y 15 es 3. Dividimos tanto el numerador como el denominador por 3, y obtenemos como resultado final 4/5.

Paso 5: Verifica tu resultado

Finalmente, siempre es importante verificar el resultado obtenido. Para ello, multiplicamos el nuevo quebrado (4/5) por el divisor original (5/6) y asegurarnos de que el producto sea igual al dividendo original (2/3). Si lo es, entonces hemos realizado la división correctamente.

Ahora que conoces este sencillo método de división de quebrados, podrás resolver problemas matemáticos con mayor facilidad. Recuerda practicar y aplicar estos pasos hasta que te sientas cómodo haciéndolo. ¡No te desesperes, la práctica hace al maestro!

Cuáles son algunos ejemplos prácticos de aplicaciones de los quebrados en la vida cotidiana

Los quebrados, también conocidos como fracciones, son una parte fundamental de las matemáticas y su aplicación se etiende más allá del aula. Aunque a simple vista pueden parecer conceptos abstractos, en realidad están presentes en numerosas situaciones cotidianas. En este artículo, te mostraremos algunos ejemplos prácticos de cómo se aplican los quebrados en la vida diaria.

1. Cocina y repostería:

Si eres amante de la cocina, seguramente has utilizado quebrados sin siquiera darte cuenta. Cuando sigues una receta, es común encontrarse con instrucciones como "1/2 taza de azúcar" o "3/4 de cucharadita de sal". Estas fracciones representan porciones de ingredientes necesarios para preparar alimentos. Además, al medir los tiempos de cocción, también puedes encontrarte con quebrados, como "1 y 1/2 horas". Así que la próima vez que estés en la cocina, ten en cuenta que los quebrados tienen un papel importante en el mundo culinario.

2. Medicina:

En el campo de la medicina, las dosis de los fármacos a menudo se epresan en forma de quebrados. Por ejemplo, si un médico receta "1/4 de pastilla" de algún medicamento, está indicando que solo debe tomarse una cuarta parte de la pastilla completa. Esto permite ajustar las dosis de manera precisa, especialmente cuando se trata de tratamientos pediátricos donde los pacientes pueden requerir dosis más pequeñas.

3. Finanzas personales:

La gestión del dinero también implica el uso de quebrados en diversos aspectos. Por ejemplo, al calcular porcentajes, los quebrados se utilizan para representar una parte proporcional de un todo. Además, al dividir el dinero entre varias personas, como al pagar la cuenta en un restaurante, es común utilizar quebrados para repartir equitativamente los gastos.

4. Arquitectura y construcción:

En el campo de la arquitectura y la construcción, los quebrados son fundamentales para las mediciones y el diseño. Por ejemplo, al medir distancias o dimensiones en planos y maquetas, es frecuente encontrarse con números que incluyen quebrados, como "1/2 metro" o "3/4 de pulgada". Estos quebrados permiten representar con precisión las proporciones y escalas de los objetos y espacios.

5. Deporte:

Incluso en el ámbito deportivo, los quebrados tienen su papel. En competiciones de atletismo, por ejemplo, se registran tiempos y velocidades utilizando quebrados. Así, los récords pueden epresarse en fracciones de segundos, como "9 y 7/10 segundos" en una carrera de 100 metros lisos. Además, también es común encontrar quebrados en estadísticas deportivas, como porcentajes de acierto en tiros libres o promedios de goles por partido.

Estos son solo algunos ejemplos de cómo se aplican los quebrados en la vida cotidiana. Como puedes ver, comprendiendo su uso y dominando su aplicación, podrás desarrollar una mayor comprensión de las matemáticas y aprovechar al máimo su utilidad en diversas situaciones prácticas.

Cómo puedes dominar la resolución de problemas con quebrados en solo 5 pasos sencillos

Los quebrados, también conocidos como fracciones, son una parte fundamental de las matemáticas. A menudo nos encontramos con problemas en los que debemos utilizar quebrados para resolverlos de manera adecuada. Sin embargo, para muchas personas, los quebrados pueden resultar confusos y difíciles de entender al principio.

En este artículo te enseñaremos cómo dominar la resolución de problemas con quebrados en tan solo 5 pasos sencillos. Sigue leyendo y descubre cómo convertirte en un eperto en el manejo de los quebrados y aplicarlos de manera eitosa en tus ejercicios matemáticos.

Paso 1: Comprender la estructura de un quebrado

Antes de poder resolver problemas con quebrados, es importante comprender su estructura básica. Un quebrado se compone de dos partes: el numerador y el denominador. El numerador representa la cantidad o parte que queremos considerar, mientras que el denominador representa el número total de partes en la unidad. Por ejemplo, en el quebrado 3/4, el numerador es 3 y el denominador es 4.

Paso 2: Identificar las operaciones a realizar

Una vez que comprendas la estructura de un quebrado, es fundamental identificar las operaciones que debes realizar en cada problema. Puedes encontrarte con problemas que requieran sumar, restar, multiplicar o dividir quebrados. Es importante leer cuidadosamente el enunciado y determinar qué tipo de operación debes utilizar.

Paso 3: Realizar las operaciones adecuadas

Una vez que identifiques las operaciones a realizar, es momento de aplicar los conocimientos matemáticos que tienes. Recuerda seguir las reglas correspondientes para cada operación con quebrados. Por ejemplo, para sumar o restar quebrados con el mismo denominador, simplemente se suman o retan los numeradores y se mantiene el denominador igual.

Paso 4: Simplificar los quebrados

En muchos casos, los quebrados pueden simplificarse para obtener una fracción en su forma más reducida. Para simplificar un quebrado, debes buscar el máimo común divisor entre el numerador y el denominador, y luego dividir ambos términos por ese número. Esto te permitirá tener una fracción más simplificada y fácil de trabajar.

Paso 5: Verificar tus resultados

El último paso, pero no menos importante, es verificar tus resultados. Una vez que hayas realizado todas las operaciones y simplificado los quebrados, asegúrate de revisar si tus respuestas son consistentes y tienen sentido en el conteto del problema. Siempre es recomendable hacer una revisión final para evitar errores y asegurarte de haber comprendido correctamente el ejercicio.

¡Y listo! Siguiendo estos 5 pasos sencillos, podrás dominar la resolución de problemas con quebrados de manera efectiva y sin complicaciones. No olvides practicar regularmente y abordar diferentes ejercicios para fortalecer tus habilidades matemáticas en este aspecto. ¡Buena suerte!

Preguntas frecuentes (FAQ)

1. ¿Qué es un quebrado en matemáticas?

Un quebrado es una epresión numérica que representa la relación de una cantidad en partes iguales.

2. ¿Cuáles son las partes de un quebrado?

Un quebrado está compuesto por un numerador, que indica el número de partes, y un denominador, que indica en cuántas partes se divide el total.

3. ¿Cómo se representa un quebrado en forma de fracción?

Un quebrado se representa como una fracción, con el numerador arriba y el denominador abajo, separados por una línea horizontal.

4. ¿Cómo se realiza la suma de quebrados?

Para sumar quebrados, debes encontrar un denominador común y luego sumar los numeradores manteniendo ese denominador común.

5. ¿Cómo se simplifica un quebrado?

Para simplificar un quebrado, debes dividir tanto el numerador como el denominador entre su máimo común divisor.