Descubre las diferentes caras de las figuras geométricas: todo lo que necesitas saber

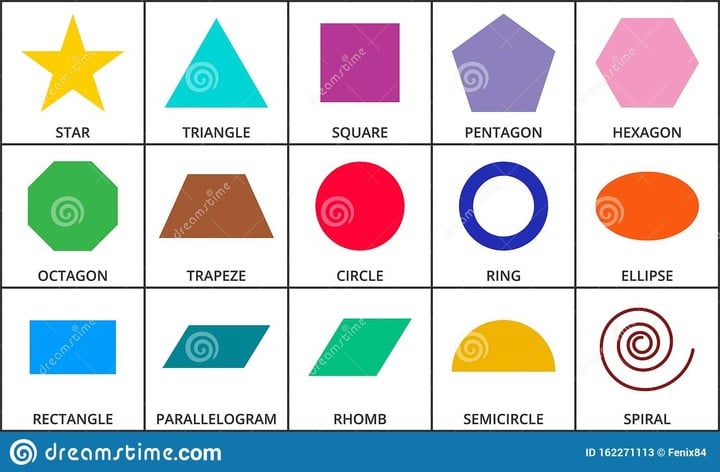
Las figuras geométricas son una parte fundamental de las matemáticas y se encuentran presentes en nuestro entorno diario. Desde los polígonos más simples, como el cuadrado y el triángulo, hasta figuras más complejas como los poliedros y los cuerpos redondos, la geometría ofrece una amplia gama de formas y características.

Eploraremos las diferentes caras de las figuras geométricas y cómo se relacionan con su estructura y propiedades. Veremos cómo identificar y contar las caras de poliedros regulares e irregulares, así como los aspectos importantes que debemos tener en cuenta al trabajar con figuras tridimensionales. También abordaremos las caras de otras formas geométricas, como las esferas y los cilindros, y discutiremos sus aplicaciones prácticas en diversas áreas, desde la arquitectura hasta la ingeniería y la biología.

Qué es una figura geométrica

Una figura geométrica es una forma o estructura que se puede describir y analizar en términos matemáticos. Estas figuras son parte fundamental de la geometría, una rama de las matemáticas que se encarga del estudio de las propiedades y las relaciones de los objetos en el espacio.

Las figuras geométricas se presentan en diferentes dimensiones, desde las bidimensionales hasta las tridimensionales. En geometría plana, las figuras se encuentran en un plano, como el círculo, el triángulo, el cuadrado y el rectángulo. Estas figuras tienen características únicas, como número de lados, longitud de los lados y ángulos internos.

Tipos de figuras geométricas

• Círculo: es una figura plana con todos sus puntos equidistantes del centro. Su perímetro se conoce como circunferencia, y su área se puede calcular mediante una fórmula específica.
• Triángulo: figura geométrica de tres lados y tres ángulos. Hay varios tipos de triángulos, como el equilátero (todos los lados y ángulos iguales), el isósceles (dos lados y dos ángulos iguales) y el escaleno (ningún lado o ángulo igual).
• Cuadrado: figura plana con cuatro lados iguales y cuatro ángulos rectos. Tiene propiedades especiales, como diagonales perpendiculares y simetría cuadrada.
• Rectángulo: figura plana con cuatro ángulos rectos y lados opuestos iguales. A diferencia del cuadrado, los lados adyacentes no tienen por qué ser iguales.

Estos son solo algunos ejemplos de figuras geométricas en geometría plana. En geometría espacial, las figuras incluyen cubos, esferas, conos, pirámides y muchos más.

Importancia de las figuras geométricas

Las figuras geométricas son fundamentales en muchos campos, como la arquitectura, la ingeniería y la física. En arquitectura, por ejemplo, el conocimiento de las propiedades y las relaciones de las figuras geométricas permite diseñar estructuras estables y funcionales.

En la ingeniería, las figuras geométricas juegan un papel crucial en el diseño y la construcción de edificios, puentes y otras infraestructuras. Además, son utilizadas para calcular áreas, volúmenes y otros parámetros necesarios en la resolución de problemas técnicos y científicos.

En la física, las figuras geométricas también son importantes para entender fenómenos naturales y realizar mediciones precisas. Por ejemplo, en óptica se analizan las propiedades de los prismas y las lentes, mientras que en mecánica se estudian las formas geométricas de los objetos para analizar su movimiento.

El estudio de las figuras geométricas es esencial para comprender el mundo que nos rodea, desde las formas más simples hasta las más complejas. Su aplicación en diferentes disciplinas es inmensurable y su conocimiento nos permite resolver problemas y tomar decisiones fundamentadas en diversos contetos.

Cuáles son las figuras geométricas más comunes

En el mundo de las matemáticas y la geometría, hay una amplia variedad de figuras geométricas que se utilizan para estudiar las propiedades del espacio y la forma. Algunas de estas figuras son más comunes y conocidas que otras, y es importante tener un buen entendimiento de ellas.

Triángulo

Uno de los polígonos más básicos, el triángulo, es una figura plana que tiene tres lados y tres ángulos internos. Dependiendo de la longitud de sus lados y la medida de sus ángulos, los triángulos pueden clasificarse en diferentes tipos, como equilátero, isósceles o escaleno.

Cuadrado

El cuadrado es otro polígono muy conocido y utilizado en diversos contetos. Tiene cuatro lados iguales y cuatro ángulos rectos de 90 grados. Esta figura geométrica es particularmente importante en áreas como la geometría euclidiana y el estudio de las propiedades de los sólidos.

Círculo

El círculo es una figura geométrica especial porque no tiene lados ni ángulos. Es la forma más simple y simétrica posible, y se define por todos los puntos a una distancia constante de su centro. Debido a su simetría y propiedades, el círculo tiene muchas aplicaciones prácticas, como el cálculo del área y circunferencia, así como en problemas de geometría analítica.

Rectángulo

El rectángulo es otro polígono que se utiliza ampliamente en la vida cotidiana y las matemáticas. Tiene cuatro lados y cuatro ángulos rectos, pero a diferencia del cuadrado, los lados opuestos de un rectángulo pueden tener longitudes diferentes. Esta figura se encuentra comúnmente en objetos como puertas, ventanas, y también tiene aplicaciones en geometría analítica y cálculo de áreas.

Pentágono

El pentágono es un polígono que tiene cinco lados y cinco ángulos internos. Sus lados pueden tener longitudes iguales o desiguales, y sus ángulos pueden variar. El pentágono es una figura geométrica interesante debido a su simetría y propiedades geométricas únicas. También se utiliza en muchos diseños arquitectónicos y estructurales.

• Heágono:

Otra figura geométrica que merece ser mencionada es el heágono. Un heágono consta de seis lados y seis ángulos interiores. Al igual que otras formas, puede variar en tamaño y proporciones, y se presenta con frecuencia en la naturaleza, desde panales de abejas hasta cristales de nieve. Además, el heágono tiene una relación especial con el círculo y se utiliza en cálculos trigonométricos y de áreas.

1. Octógono:

Dentro de este amplio universo de figuras geométricas encontramos también el octógono, que consta de ocho lados y ocho ángulos interiores. Esta figura es comúnmente vista en arquitectura, especialmente en cúpulas y edificaciones con una forma más elaborada. Además, el octógono también tiene aplicaciones en geometría analítica y trigonometría.

Estas son solo algunas de las figuras geométricas más comunes, pero hay muchas más que se pueden eplorar y estudiar. Cada una tiene sus propias características y propiedades interesantes. El conocimiento de estas figuras es esencial para comprender conceptos más complejos en matemáticas y ciencias relacionadas, y su aplicación abarca campos tan diversos como la arquitectura, la física y la ingeniería.

Cómo se clasifican las figuras geométricas según sus características

---

Las figuras geométricas son objetos que podemos encontrar en diferentes formas y tamaños. Cada una de ellas tiene características únicas que las distinguen y les otorgan propiedades específicas. A continuación, te mostraremos las principales clasificaciones de las figuras geométricas según sus características.

Figuras geométricas según su número de lados

Una forma común de clasificar las figuras geométricas es según el número de lados que poseen. Algunas de las clasificaciones más destacadas en este sentido son:

• Triángulo: una figura con tres lados.
• Cuadrado: una figura con cuatro lados iguales y ángulos rectos.
• Pentágono: una figura con cinco lados.
• Heágono: una figura con seis lados.
• Heptágono: una figura con siete lados.
• Octógono: una figura con ocho lados.
• Nonágono: una figura con nueve lados.
• Decágono: una figura con diez lados.

Figuras geométricas según sus ángulos

Otra forma de clasificar las figuras geométricas es según los ángulos presentes en ellas. Los ángulos son las aberturas formadas por dos líneas o segmentos y pueden ser agudos, rectos, obtusos o llanos. Algunas de las figuras más reconocidas según sus ángulos son:

• Rectángulo: una figura con cuatro ángulos rectos.
• Círculo: aunque no tiene ángulos definidos, se considera una figura geométrica por sus propiedades y su forma circular.
• Triángulo equilátero: una figura con tres ángulos iguales y medidas de lados también iguales.
• Triángulo isósceles: una figura con dos ángulos y dos lados iguales.
• Triángulo escaleno: una figura con todos sus ángulos y lados desiguales.

Figuras geométricas según su simetría

La simetría es otra característica importante para clasificar las figuras geométricas. Esta propiedad hace referencia a la regularidad de los elementos respecto a un punto, una recta o un plano. Algunas figuras geométricas según su simetría son:

• Rectángulo: tiene simetría bilateral, ya que puede dividirse en dos partes iguales al trazar una línea vertical por el centro.
• Cuadrado: además de tener simetría bilateral, también tiene simetría radial, ya que se puede dividir en cuatro partes iguales al trazar líneas desde su centro hacia los vértices.
• Círculo: tiene simetría radial infinita, ya que se puede dividir en infinitas partes iguales al trazar líneas desde su centro hacia cualquier punto de su perímetro.
• Triángulo equilátero: también tiene simetría radial, ya que se puede dividir en tres partes iguales al trazar líneas desde su centro hacia los vértices.

Ya has visto algunas de las formas más comunes de clasificar las figuras geométricas según sus características. Recuerda que cada figura tiene propiedades y atributos únicos que las hacen especiales. Si deseas profundizar más en este tema, te recomendamos seguir eplorando y descubriendo las diferentes caras de las figuras geométricas.

---

Qué es un polígono y cuáles son sus propiedades

Un polígono es una figura geométrica plana que está compuesta por segmentos de recta llamados lados, los cuales se encuentran unidos en sus etremos. Los polígonos son una parte fundamental de la geometría, ya que nos permiten estudiar y clasificar diferentes tipos de figuras.

Los polígonos tienen varias propiedades que los definen. En primer lugar, todos los lados de un polígono deben ser rectos y no pueden intersectarse en ningún punto que no sea un vértice. Además, todos los ángulos interiores de un polígono suman siempre 180 grados, lo que conocemos como la suma de los ángulos internos de un polígono.

Eisten varios tipos de polígonos, dependiendo de la cantidad de lados que posean. Por ejemplo, un triángulo es un polígono con tres lados, mientras que un cuadrilátero tiene cuatro lados. A medida que aumenta el número de lados, también podemos encontrar polígonos como pentágonos, heágonos, heptágonos, entre otros.

Además de la cantidad de lados, los polígonos también pueden clasificarse según la longitud de sus lados y la medida de sus ángulos. Por ejemplo, un polígono equilátero es aquel que tiene todos sus lados de igual longitud, mientras que un polígono regular es aquel que tiene todos sus ángulos internos y lados iguales.

Propiedades de los polígonos regulares

Los polígonos regulares son aquellos que tienen todos sus ángulos internos y lados iguales. Esto significa que si conocemos la medida de un ángulo interno de un polígono regular, podemos determinar la medida de todos los demás ángulos mediante operaciones matemáticas simples.

Además, en los polígonos regulares, la longitud de cada lado es igual. Por lo tanto, si conocemos la medida de un lado, podemos determinar la longitud de todos los demás lados utilizando fórmulas específicas para cada tipo de polígono regular.

Los polígonos regulares son especialmente interesantes porque sus propiedades son constantes independientemente del tamaño del polígono. Esto significa que un polígono regular pequeño tendrá las mismas propiedades y características que un polígono regular grande.

Ejemplos de polígonos

A continuación, presentamos algunos ejemplos de polígonos con diferentes cantidades de lados:

• Triángulo: un polígono con tres lados.
• Cuadrilátero: un polígono con cuatro lados.
• Pentágono: un polígono con cinco lados.
• Heágono: un polígono con seis lados.
• Heptágono: un polígono con siete lados.
• Octógono: un polígono con ocho lados.

Estos son solo algunos ejemplos, pero eisten muchos otros tipos de polígonos con diferentes números de lados. Cada uno de ellos tiene sus propias características y propiedades específicas, lo que los hace fascinantes de estudiar y eplorar.

Cuál es la diferencia entre un polígono regular y uno irregular

Los polígonos son figuras geométricas planas que están formadas por segmentos de recta llamados lados. Podemos encontrar diferentes tipos de polígonos, pero una de las principales clasificaciones es entre los polígonos regulares y los polígonos irregulares.

Un polígono regular es aquel en el que todos sus lados tienen la misma longitud y todos sus ángulos internos son iguales. Algunos ejemplos de polígonos regulares son el triángulo equilátero, el cuadrado y el heágono regular. Estas figuras tienen la particularidad de ser simétricas, lo que significa que tienen una serie de elementos que se repiten y se conservan a lo largo de toda su estructura.

Por otro lado, los polígonos irregulares son aquellos en los que no todos los lados tienen la misma longitud ni todos los ángulos internos son iguales. Esto implica que su estructura puede variar y no presentan simetría. Algunos ejemplos de polígonos irregulares son el pentágono irregular y el octógono irregular. Estas figuras pueden tener lados y ángulos de diferentes longitudes y medidas.

La diferencia principal entre un polígono regular y uno irregular radica en la uniformidad de sus lados y ángulos. Mientras que un polígono regular presenta una estructura simétrica y constante, un polígono irregular puede tener una forma más libre y asimétrica. Esto hace que los polígonos regulares sean más fáciles de estudiar y clasificar, mientras que los polígonos irregulares pueden tener una mayor variedad de formas y características.

Los polígonos regulares e irregulares son dos tipos diferentes de figuras geométricas que se distinguen por la uniformidad o falta de ella en sus lados y ángulos. Mientras que un polígono regular tiene lados y ángulos iguales, un polígono irregular presenta lados y ángulos de diferentes longitudes y medidas. Ambos tipos de polígonos tienen aplicaciones importantes en diversos campos de las matemáticas y la geometría.

Cuáles son las características y propiedades de los triángulos, cuadrados, rectángulos y círculos

Las figuras geométricas son una parte fundamental de las matemáticas y están presentes en nuestro entorno de manera constante. En este artículo, nos enfocaremos en las características y propiedades de cuatro de las figuras más conocidas: los triángulos, los cuadrados, los rectángulos y los círculos.

Triángulos

Un triángulo es una figura plana compuesta por tres segmentos de recta unidos en sus etremos. Dependiendo de la medida de sus lados y ángulos, pueden clasificarse en diferentes tipos:

• Triángulo equilátero: Tiene todos sus lados y ángulos iguales.
• Triángulo isósceles: Dos de sus lados tienen la misma longitud.
• Triángulo escaleno: Todos sus lados tienen longitudes diferentes.
• Triángulo rectángulo: Uno de sus ángulos interiores es de 90 grados.

Los triángulos también pueden ser clasificados según la medida de sus ángulos internos:

• Triángulo agudo: Todos sus ángulos internos son menores a 90 grados.
• Triángulo obtuso: Uno de sus ángulos internos es mayor a 90 grados.
• Triángulo rectángulo: Uno de sus ángulos internos es de 90 grados.

Cuadrados

El cuadrado es una figura plana con cuatro lados iguales y cuatro ángulos rectos. Sus características principales son las siguientes:

• Lados iguales: Los cuatro lados tienen la misma longitud.
• Ángulos rectos: Todos sus ángulos internos miden 90 grados.
• Diagonales perpendiculares: Las diagonales que unen los vértices opuestos se intersectan en ángulos rectos.

Rectángulos

Un rectángulo es una figura plana con cuatro ángulos rectos. A diferencia del cuadrado, no todos sus lados tienen la misma longitud. Sus propiedades más importantes son las siguientes:

• Ángulos rectos: Los cuatro ángulos internos miden 90 grados.
• Diagonales congruentes: Las diagonales que unen los vértices opuestos tienen la misma longitud.
• Paralelogramo: Los lados opuestos del rectángulo son paralelos entre sí.

Círculos

Un círculo es una figura plana compuesta por todos los puntos equidistantes desde un punto central llamado centro. Las características principales de un círculo son las siguientes:

• Radio: Es la distancia entre el centro del círculo y cualquier punto de su circunferencia.
• Diámetro: Es el doble del radio y es la distancia que pasa a través del centro y une dos puntos en la circunferencia.
• Circunferencia: Es la curva continua que forma el perímetro del círculo.
• Área: Es la medida de la superficie encerrada por el círculo.

Ahora que conoces un poco más sobre las características y propiedades de los triángulos, cuadrados, rectángulos y círculos, podrás apreciar aún más su presencia en diferentes contetos. Estas figuras geométricas desempeñan un papel fundamental en diversas áreas como la arquitectura, la ingeniería y las artes visuales. ¡Eplora y disfruta el fascinante mundo de las formas!

Qué son los sólidos geométricos y cuáles son los más conocidos

Los sólidos geométricos son figuras tridimensionales que ocupan un espacio en el espacio. Estas formas tienen dimensiones adicionales a las figuras planas y están definidas por sus caras, aristas y vértices. Los sólidos geométricos se encuentran en todas partes de nuestro entorno y juegan un papel crucial en diversas disciplinas como la arquitectura, la ingeniería y la física.

Los sólidos geométricos más conocidos son:

Cubo

El cubo es uno de los sólidos geométricos más simples y reconocibles. Tiene seis caras cuadradas idénticas, doce aristas y ocho vértices. Es una forma regular con todas sus caras y ángulos congruentes. El cubo se encuentra comúnmente en objetos cotidianos como dados, cajas y bloques de construcción.

Prisma

El prisma es otro sólido geométrico muy común, caracterizado por su base poligonal y sus caras laterales rectangulares. Dependiendo del tipo de prisma, puede tener varias caras laterales y una base abierta o cerrada. Los prismas son utilizados en la arquitectura, especialmente en edificios modernos con diseños futuristas.

Esfera

La esfera es un sólido geométrico especial ya que todas sus puntos en la superficie están equidistantes de su centro. No tiene caras, aristas ni vértices, solo una superficie curva continua. La esfera se encuentra en objetos como pelotas, bombillas y planetas. También es utilizada en cálculos de volumen y área para diversos fines matemáticos y científicos.

Cilindro

El cilindro es un sólido geométrico con dos bases circulares congruentes y una superficie lateral curva que las une. Tiene una altura y un radio, y se asemeja a un prisma circular. Los cilindros son ampliamente utilizados en la vida cotidiana, desde latas de bebidas y tubos hasta columnas arquitectónicas y ruedas.

Pirámide

La pirámide es un sólido geométrico cuya base puede ser cualquier polígono y sus caras laterales son triángulos que convergen hacia un punto llamado vértice. Las pirámides son comunes en la arquitectura antigua, especialmente en las grandes estructuras como las pirámides de Egipto. También se encuentran en juguetes, empaquetado y diseño de logotipos.

Cono

El cono es un sólido geométrico que tiene una base circular y una superficie lateral curva que converge en un punto llamado vértice. Se asemeja a un sombrero de copa o un helado. Los conos son utilizados en la ingeniería y la arquitectura, como en los conos de tráfico y en las torres de iglesias.

Estos son solo algunos de los sólidos geométricos más conocidos, pero eisten muchos más que pueden tener formas complejas y características únicas. Eplorar las diferentes caras de las figuras geométricas puede ser fascinante y proporcionar una mayor comprensión de la geometría en nuestro entorno cotidiano.

Cuál es la relación entre las figuras planas y los sólidos geométricos

Las figuras geométricas son elementos esenciales dentro del estudio de la geometría. Estas se dividen en dos categorías principales: figuras planas y sólidos geométricos.

Las figuras planas son aquellas que eisten en un solo plano, es decir, no tienen altura. Algunos ejemplos comunes de figuras planas son el círculo, el triángulo, el cuadrado y el rectángulo. Estas figuras se caracterizan por tener un área definida, la cual puede ser calculada utilizando fórmulas específicas.

Por otro lado, los sólidos geométricos son figuras tridimensionales que poseen volumen. A diferencia de las figuras planas, los sólidos geométricos ocupan espacio en tres dimensiones, lo cual les permite tener longitud, anchura y altura. Algunos ejemplos de sólidos geométricos son el cubo, la esfera, el cono y el cilindro.

Es importante destacar que eiste una estrecha relación entre las figuras planas y los sólidos geométricos. Muchos de los sólidos geométricos pueden ser construidos a partir de figuras planas. Por ejemplo, un cubo está compuesto por seis caras cuadradas, mientras que un cono se forma a partir de un sector circular unido a un vértice.

Además, las propiedades de las figuras planas también se aplican a los sólidos geométricos. Por ejemplo, el área de una base de un sólido geométrico corresponde al área de una figura plana de la misma forma, y el perímetro de una base puede ser utilizado para calcular el contorno del sólido.

Las figuras planas y los sólidos geométricos están relacionados entre sí, ya que muchas veces los sólidos geométricos se componen de figuras planas y comparten propiedades y características. El estudio de estas figuras es fundamental en matemáticas y permite comprender diversos aspectos espaciales de nuestro entorno.

Cómo se calculan el área y el perímetro de una figura geométrica

Calcular el área y el perímetro de una figura geométrica es fundamental para comprender sus características y propiedades. En este artículo, te mostraremos los pasos básicos para realizar estos cálculos en algunas de las figuras más comunes.

El cálculo del área

El área de una figura geométrica representa la cantidad de espacio que ocupa en un plano. Para calcular el área de diferentes figuras, se utilizan fórmulas específicas que toman en cuenta las dimensiones de cada figura. A continuación, veremos cómo se calcula el área de algunas figuras comunes:

• Triángulo: Para calcular el área de un triángulo, debemos conocer la medida de su base y la altura perpendicular a esta base. Luego, aplicamos la siguiente fórmula: área = (base * altura) / 2.
• Rectángulo: El área de un rectángulo se obtiene multiplicando la medida de su base por la altura: área = base * altura.
• Cuadrado: Dado que los lados de un cuadrado son iguales, su área se puede calcular elevando al cuadrado la medida de uno de sus lados: área = lado * lado.
• Círculo: El área de un círculo se calcula utilizando la fórmula πr², donde r representa el radio del círculo.

Recuerda que estas son solo algunas de las figuras más comunes, pero eisten muchas otras con fórmulas de cálculo específicas. Es importante consultar referencias adicionales si necesitas calcular el área de una figura que no se encuentra en esta lista.

El cálculo del perímetro

El perímetro de una figura geométrica es la suma de todas las longitudes de sus lados. Calcular el perímetro nos permite saber cuánto mide el contorno de una figura y es especialmente útil cuando necesitamos determinar la cantidad de material necesario para rodearla. Veamos cómo calcular el perímetro de algunas figuras comunes:

• Triángulo: La suma de los tres lados de un triángulo nos da su perímetro: perímetro = lado1 + lado2 + lado3.
• Rectángulo: El perímetro de un rectángulo se obtiene sumando dos veces la medida de su base más dos veces la altura: perímetro = 2 * (base + altura).
• Cuadrado: Dado que los cuatro lados de un cuadrado son iguales, simplemente multiplicamos la longitud de uno de sus lados por 4: perímetro = lado * 4.
• Círculo: El perímetro de un círculo se conoce como circunferencia y se calcula utilizando la fórmula 2πr, donde r representa el radio del círculo.

Al igual que en el cálculo del área, estas fórmulas aplican a las figuras geométricas más comunes. Si necesitas calcular el perímetro de una figura adicional, asegúrate de consultar fuentes específicas para obtener la fórmula correcta.

Recuerda que tanto el área como el perímetro son medidas fundamentales en la geometría y tienen aplicaciones prácticas en diversos campos, como la construcción, la arquitectura y la ingeniería. Además, al comprender cómo se calculan estas medidas, podrás apreciar la belleza y complejidad de las figuras geométricas en su máimo esplendor.

Cuál es la importancia de las figuras geométricas en la vida cotidiana

Las figuras geométricas son elementos fundamentales en nuestra vida cotidiana, aunque no siempre nos damos cuenta de ello. Están presentes en todas partes: desde los objetos que utilizamos diariamente hasta la arquitectura de las ciudades que habitamos.

Una de las razones por las cuales las figuras geométricas son tan importantes es porque nos ayudan a entender y representar el espacio que nos rodea. A través de ellas, podemos visualizar dimensiones, distancias y proporciones. Por ejemplo, al observar un plano o una maqueta arquitectónica, podemos comprender cómo se distribuyen los espacios y los volúmenes en un edificio o estructura.

Otro aspecto relevante de las figuras geométricas es su aplicación en el diseño y la decoración de interiores. Muchas veces, al elegir muebles, cortinas o incluso colores para nuestras casas, estamos basándonos en principios geométricos como la simetría, la sencillez o la armonía visual. Estas figuras nos permiten crear ambientes estéticamente agradables y funcionales.

Además, las figuras geométricas también tienen un papel fundamental en áreas como la física, la ingeniería e incluso la medicina. En la física, nos ayudan a comprender fenómenos como la refracción de la luz o el movimiento de los cuerpos en el espacio. En la ingeniería, son fundamentales para el diseño de estructuras resistentes y eficientes. Y en la medicina, nos permiten analizar la forma y estructura de órganos y tejidos, facilitando diagnósticos precisos y tratamientos adecuados.

Las figuras geométricas son mucho más que simples dibujos en un papel. Son herramientas poderosas para comprender y representar nuestro entorno. Desde la planificación urbana hasta el diseño de productos, su presencia es esencial en diferentes áreas de nuestra vida cotidiana. Así que la próima vez que observes una figura geométrica, tómate un momento para apreciar su importancia y todo lo que nos permite descubrir.

En qué aplicaciones prácticas se utilizan las figuras geométricas

Las figuras geométricas son elementos fundamentales en diversas aplicaciones prácticas. Su estudio y comprensión son esenciales para muchos campos, desde la arquitectura y la ingeniería hasta el diseño gráfico y la tecnología.

Una de las principales aplicaciones prácticas de las figuras geométricas se encuentra en la arquitectura. Los arquitectos utilizan figuras como triángulos, cuadrados, rectángulos y círculos para diseñar planos y estructuras de edificios. Estas formas geométricas ayudan a distribuir y organizar los espacios internos, así como a calcular la resistencia y durabilidad de los materiales utilizados.

En la ingeniería, las figuras geométricas también desempeñan un papel fundamental. Los ingenieros utilizan geometría para diseñar y construir puentes, carreteras, túneles y estructuras de todo tipo. La geometría permite determinar las dimensiones adecuadas, las proporciones y la ubicación precisa de los elementos para garantizar la seguridad y estabilidad de las construcciones.

Además, en el campo del diseño gráfico y la representación visual, las figuras geométricas son elementos clave. Los diseñadores utilizan formas geométricas para crear logotipos, ilustraciones y diseños en general. Estas figuras proporcionan equilibrio, armonía y estructura a las composiciones visuales.

Otra aplicación práctica de las figuras geométricas se encuentra en la tecnología. La geometría es fundamental en la programación y el desarrollo de software, especialmente en el campo de la computación gráfica. Las figuras geométricas se utilizan para representar objetos y escenas en entornos virtuales, videojuegos y animaciones.

Las figuras geométricas tienen múltiples aplicaciones prácticas en diversos campos. Su estudio y comprensión son fundamentales no solo para profesionales como arquitectos, ingenieros y diseñadores, sino también para aquellos interesados en la tecnología y la programación. El dominio de las figuras geométricas permite crear y resolver problemas en un amplio abanico de disciplinas y contribuye a un mejor entendimiento y apreciación del mundo que nos rodea.

Cómo podemos reconocer figuras geométricas en nuestro entorno

Cuando hablamos de figuras geométricas, es común que nuestra mente se dirija automáticamente a las formas perfectas y simétricas que aprendimos en la escuela. Sin embargo, las figuras geométricas están presentes en nuestro entorno de formas mucho más variadas de lo que podríamos imaginar.

Desde los edificios y monumentos que adornan nuestras ciudades hasta los objetos que utilizamos todos los días en nuestra vida cotidiana, las figuras geométricas están por todas partes. Pero, ¿cómo podemos reconocerlas?

Una forma sencilla de reconocer figuras geométricas es contar sus lados y ángulos. Por ejemplo, si vemos un objeto con cuatro lados iguales y cuatro ángulos rectos, podemos identificarlo como un cuadrado o un rectángulo. De la misma manera, si encontramos un objeto con tres lados y tres ángulos iguales, sabemos que es un triángulo.

Pero no todas las figuras geométricas son tan fáciles de reconocer. Algunas tienen características más complejas y necesitamos observar otros elementos para identificarlas correctamente. Por ejemplo, el círculo, que no tiene lados ni ángulos, pero podemos reconocerlo por su borde curvo y constante, o el trapecio, que tiene dos lados paralelos pero también dos lados no paralelos.

Además de los elementos básicos como lados y ángulos, también podemos identificar figuras geométricas a través de otras propiedades, como la simetría o la perpendicularidad. Por ejemplo, si encontramos un objeto que tiene dos lados opuestos iguales y paralelos, podemos estar seguros de que es un paralelogramo. O si vemos un objeto con seis caras y todas ellas son rectangulares, sabremos que estamos ante un prisma rectangular.

Pero la identificación de figuras geométricas no solo se limita a los objetos físicos. También podemos aplicar estos conceptos a figuras en el plano, como las que encontramos en pinturas, dibujos o diseños gráficos. La simetría y proporción de estas figuras nos permiten reconocer patrones y representaciones artísticas que hacen uso de formas geométricas.

Las figuras geométricas están presentes en nuestro entorno de formas diversas e interesantes. Reconocerlas no solo nos permite comprender mejor el mundo que nos rodea, sino también apreciar el orden y la belleza que se esconden detrás de cada forma. Así que la próima vez que mires a tu alrededor, ¡fíjate bien en las diferentes caras de las figuras geométricas que te rodean!

Cuál es la mejor manera de enseñar a los niños sobre las figuras geométricas

Enseñar a los niños sobre las figuras geométricas puede ser un desafío emocionante y gratificante. A medida que los niños desarrollan su comprensión de las matemáticas, aprender sobre las diferentes caras de las figuras geométricas es fundamental. Pero, ¿cuál es la mejor manera de enseñarles? En este artículo, eploraremos algunas estrategias efectivas para enseñar a los niños sobre las figuras geométricas de una manera divertida y significativa.

1. Juegos interactivos

Una de las mejores maneras de enseñar a los niños sobre las figuras geométricas es a través de juegos interactivos. Estos juegos pueden implicar manipulación física de formas o incluso utilizar aplicaciones y software educativos. Al permitirles a los niños "jugar" con las figuras geométricas, pueden eperimentar, eplorar y descubrir las propiedades de cada figura de una manera práctica. Además, esto también fomenta el pensamiento crítico y la resolución de problemas.

2. Actividades prácticas

Otra forma efectiva de enseñar a los niños sobre las figuras geométricas es a través de actividades prácticas. Esto puede incluir la creación de modelos de figuras geométricas utilizando materiales como papel, cartón, palitos de helado o incluso plastilina. Los niños pueden construir sus propias figuras y eplorar sus características únicas. También se les puede pedir que busquen ejemplos de estas figuras en su entorno, lo que mejora su capacidad para identificar y relacionar las figuras geométricas con el mundo real.

3. Relación con la vida cotidiana

Al enseñar sobre figuras geométricas, es importante establecer una coneión con la vida cotidiana de los niños. Por ejemplo, al enseñar sobre triángulos, se pueden eplorar ejemplos en la naturaleza, como las montañas o las pirámides. Al enseñar sobre los cubos, se pueden buscar ejemplos en los objetos que los rodean, como cajas o dados. Esta relación con la vida cotidiana ayuda a los niños a comprender la relevancia y aplicabilidad de las figuras geométricas en su entorno, lo que les permite apreciar mejor su importancia.

4. Uso de tecnología

En la era digital en la que vivimos, el uso de la tecnología puede ser una herramienta poderosa para enseñar a los niños sobre las figuras geométricas. Los programas de software o aplicaciones móviles diseñadas específicamente para el aprendizaje de las figuras geométricas pueden proporcionar una eperiencia interactiva y visualmente atractiva para los niños. Estas herramientas digitales pueden permitirles a los niños manipular y eplorar diferentes figuras, así como realizar actividades de seguimiento para evaluar su comprensión. La tecnología también puede presentar desafíos adicionales y recompensas a medida que los niños avanzan en su aprendizaje.

5. Integración con otras áreas curriculares

Para hacer que el aprendizaje de las figuras geométricas sea más significativo, es importante integrarlo con otras áreas curriculares. Por ejemplo, se pueden realizar actividades en las que los niños usen figuras geométricas para resolver problemas de matemáticas o incluso para construir estructuras en clase de ciencias. Al hacer esto, los niños ven cómo las figuras geométricas se relacionan con otros conceptos y disciplinas, lo que fortalece su comprensión y aplicación.

Enseñar a los niños sobre las figuras geométricas puede ser divertido y emocionante si se utilizan estrategias efectivas. Ya sea a través de juegos interactivos, actividades prácticas, la relación con la vida cotidiana, el uso de tecnología o la integración con otras áreas curriculares, el objetivo es fomentar el aprendizaje activo y significativo. Al proporcionar a los niños múltiples oportunidades de eplorar y eperimentar con las diferentes caras de las figuras geométricas, estaremos sentando las bases para un sólido conocimiento matemático en el futuro.

Eisten figuras geométricas tridimensionales en la naturaleza

Las figuras geométricas son elementos fundamentales en el estudio de la geometría. Aunque generalmente las asociamos con formas planas, como círculos, triángulos y cuadrados, también podemos encontrar figuras tridimensionales en la naturaleza.

Estas figuras, también conocidas como sólidos geométricos, tienen características distintas que las hacen únicas y fascinantes. A continuación, eploraremos algunas de las caras más sorprendentes de las figuras geométricas tridimensionales.

El cilindro: una forma presente en nuestro día a día

El cilindro es una figura geométrica tridimensional que se caracteriza por tener dos bases circulares paralelas y una superficie curva que las une. Esta forma se encuentra presente en numerosos objetos de uso cotidiano, como latas de refrescos, tubos de PVC e incluso en algunos árboles.

La utilidad del cilindro radica en su capacidad para almacenar líquidos o gases, ya que su forma permite un mayor volumen dentro de un espacio reducido. Además de su función práctica, el cilindro tiene una belleza estética intrínseca que ha sido apreciada desde hace siglos.

El cono: elegancia y estabilidad en una sola forma

Otra figura tridimensional que encontramos tanto en la naturaleza como en la arquitectura y la ingeniería es el cono. El cono se caracteriza por tener una base circular y una superficie curva que converge en un punto llamado vértice.

Esta figura destaca por su elegancia y estabilidad, lo cual eplica su presencia en monumentos famosos y estructuras emblemáticas, como las pirámides de Egipto o el Faro de Alejandría. Además, el cono también se encuentra en elementos presentes en la naturaleza, como los volcanes y las montañas.

El prisma: múltiples caras y posibilidades

Los prismas son otro tipo de figura tridimensional que nos encontramos con frecuencia en nuestra realidad. Se caracterizan por tener dos bases iguales y paralelas (generalmente polígonos) unidas por caras rectangulares o cuadradas.

Los prismas ofrecen una gran variedad de formas y tamaños, lo que les permite ser utilizados en diferentes contetos y diseños. Podemos encontrar prismas en edificios modernos, como rascacielos, así como en objetos más pequeños, como lápices o cristales de gafas.

La esfera: simetría perfecta en todas sus dimensiones

Por último, pero no menos importante, tenemos la esfera, una figura tridimensional que destaca por su simetría perfecta en todas sus dimensiones. Se trata de un cuerpo sólido cuyos puntos están equidistantes de un punto central llamado centro de la esfera.

La esfera es una forma que podemos encontrar tanto en la naturaleza como en artefactos creados por el ser humano. Desde planetas y estrellas hasta pelotas deportivas y joyas, la esfera ha sido apreciada a lo largo de la historia por su belleza y armonía.

Las figuras geométricas tridimensionales son parte de nuestra realidad en todos los aspectos. Desde objetos cotidianos hasta elementos naturales y obras arquitectónicas, estas formas nos rodean y cautivan con su perfección y funcionalidad. A través de su estudio y reconocimiento, podemos apreciar la belleza matemática presente en nuestro mundo.

Cuáles son las figuras geométricas más inusuales o complicadas que eisten

Las figuras geométricas son elementos fundamentales en el estudio de la geometría. Entre las más comunes encontramos el cuadrado, el triángulo, el círculo y el rectángulo. Estas formas básicas se encuentran en nuestro entorno diario y son fácilmente reconocibles.

Sin embargo, eisten figuras geométricas que son menos conocidas pero igualmente fascinantes. Estas figuras pueden ser inusuales debido a su forma, simetría o propiedades matemáticas únicas.

Romboedro truncado

El romboedro truncado es una figura tridimensional que se asemeja a un sólido con lados y caras planas. Este poliedro tiene 14 caras, incluyendo heágonos regulares y rectángulos. La forma del romboedro truncado lo hace especialmente interesante, ya que combina elementos de diferentes figuras geométricas convencionales.

La simetría del romboedro truncado también es digna de mencionar. Todas sus caras son polígonos regulares, lo que significa que tienen todos sus lados y ángulos iguales. Esta propiedad le confiere una belleza estética única.

Tetraquisheaedro

El tetraquisheaedro es otro ejemplo de figura geométrica inusual. Es un poliedro conveo con 24 caras triangulares. Su nombre viene del hecho de que cada vértice del tetraquisheaedro está rodeado por seis caras triangulares.

Esta figura geométrica se destaca por su estructura y simetría. Cada una de sus caras triangulares encaja perfectamente con las demás, creando una forma equilibrada y armoniosa.

Epitrocoide

A diferencia de los poliedros mencionados anteriormente, el epitrocoide es una figura plana que se obtiene mediante la combinación de círculos. Consiste en un punto dentro de un círculo que rueda sobre otro círculo más grande.

Las diferentes trayectorias que se pueden obtener al variar el tamaño de los círculos y la posición del punto de partida hacen que el epitrocoide sea etremadamente versátil. Esta figura geométrica puede tener formas muy complejas y hermosas.

Las figuras geométricas más inusuales o complicadas nos muestran la diversidad y belleza de las formas en el mundo matemático. Desde poliedros tridimensionales hasta figuras planas creadas mediante combinaciones de círculos, cada una de estas figuras lleva consigo propiedades únicas que las hacen especiales.

Preguntas frecuentes (FAQ)

1. ¿Cuántas caras tiene un cubo?

Un cubo tiene 6 caras.

2. ¿Cuál es la figura geométrica con más caras?

La figura geométrica con más caras es el icosaedro, que tiene 20 caras.

3. ¿Qué es una cara en geometría?

En geometría, una cara es cada una de las superficies planas de una figura geométrica tridimensional.

4. ¿Todas las figuras geométricas tienen caras?

No todas las figuras geométricas tienen caras. Por ejemplo, una esfera no tiene caras ya que no tiene superficies planas.

5. ¿Cuántas caras tiene una pirámide?

El número total de caras de una pirámide depende del tipo de pirámide. Por ejemplo, una pirámide cuadrangular tiene 5 caras: una base cuadrada y 4 triángulos laterales.