¡Descubre cuál de los siguientes triángulos tiene un ángulo obtuso en solo 3 pasos!
Los triángulos son una figura geométrica que consta de tres lados y tres ángulos. Dependiendo de la medida de sus ángulos, los triángulos pueden clasificarse en diferentes tipos, como equilátero, isósceles o escaleno. Uno de estos tipos es el triángulo obtuso, el cual tiene un ángulo mayor a 90 grados.
En este artículo te eplicaremos cómo identificar fácilmente si un triángulo tiene un ángulo obtuso en solo 3 pasos. Esta información puede ser útil para resolver problemas de geometría o simplemente para ampliar tus conocimientos sobre figuras geométricas. Sigue leyendo para aprender más sobre este interesante tema.
- Qué es un ángulo obtuso
- Cómo identificar un ángulo obtuso en un triángulo
- Cuál es la importancia de identificar los ángulos obtusos en un triángulo
- Cuáles son los diferentes tipos de triángulos y sus características
- Cómo se puede determinar si un triángulo tiene un ángulo obtuso en solo 3 pasos
- Cuál es el primer paso para identificar un ángulo obtuso en un triángulo
- Cuáles son las medidas de los ángulos en un triángulo rectángulo
- Cuál es el segundo paso para identificar un ángulo obtuso en un triángulo
- Qué es un triángulo equilátero y cómo se relaciona con los ángulos
- Cuál es el tercer paso para identificar un ángulo obtuso en un triángulo
- Cuáles son algunos ejemplos de triángulos que tienen un ángulo obtuso
- Por qué es importante entender los ángulos obtusos en la geometría
- Cómo se pueden utilizar los ángulos obtusos en aplicaciones del mundo real
- Preguntas frecuentes (FAQ)
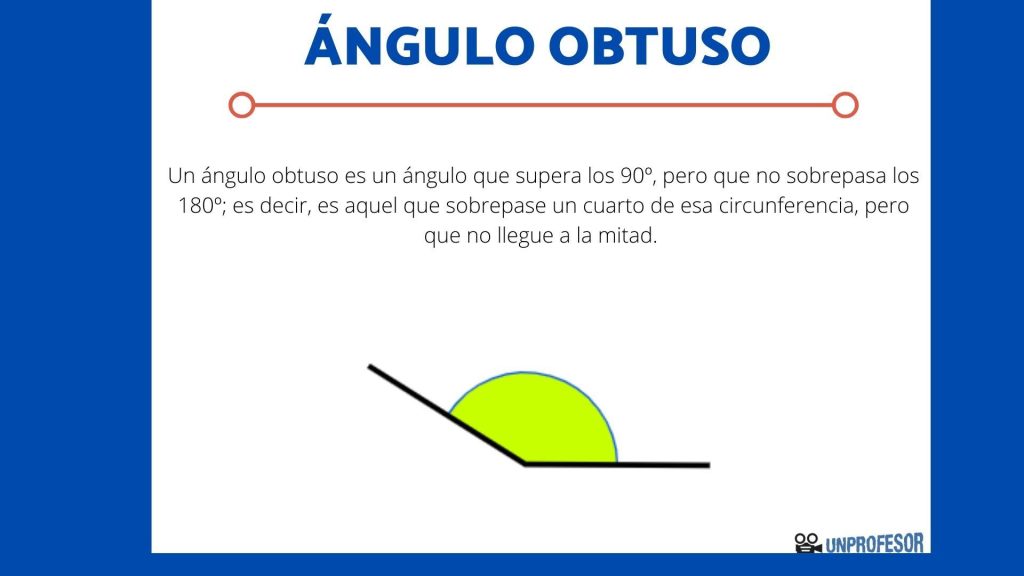
Qué es un ángulo obtuso
Un ángulo obtuso es aquel que mide más de 90 grados pero menos de 180 grados. En otras palabras, es un ángulo más grande que un ángulo recto (90 grados) pero más pequeño que un ángulo llano (180 grados). Los ángulos obtusos suelen ser caracterizados por su apertura, ya que se etienden más allá de la perpendicularidad, pero sin llegar a ser completamente planos como los ángulos llanos.
Cómo identificar un ángulo obtuso
Identificar si un ángulo es obtuso o no puede ser una tarea sencilla si se siguen algunos pasos y se conocen las propiedades básicas de los triángulos. A continuación, te eplicaré cómo puedes hacerlo en solo 3 pasos:
- Paso 1: Medir los ángulos del triángulo
- Paso 2: Comparar las medidas
- Paso 3: Identificar el ángulo obtuso
Lo primero que debes hacer es medir los ángulos del triángulo en cuestión. Puedes utilizar un transportador de ángulos o una regla con un transportador incorporado para obtener medidas precisas.
Una vez que tengas las medidas de los tres ángulos del triángulo, compáralas entre sí. Recuerda que para que un triángulo tenga un ángulo obtuso, al menos uno de sus ángulos debe ser mayor a 90 grados.
Si encuentras que uno de los ángulos del triángulo es mayor a 90 grados, has identificado el ángulo obtuso. Puedes resaltar este ángulo en tu figura o anotarlo claramente en la descripción del triángulo.
Ahora que sabes cómo identificar un ángulo obtuso en un triángulo, ¡pon a prueba tus conocimientos! A continuación, se presentan varios ejemplos de triángulos. Tú tarea es encontrar cuál de ellos tiene al menos un ángulo obtuso. Recuerda seguir los pasos descritos anteriormente y no olvides medir cuidadosamente los ángulos antes de tomar tu decisión.
Cómo identificar un ángulo obtuso en un triángulo
Identificar si un triángulo tiene un ángulo obtuso puede parecer complicado, pero en realidad se puede hacer en tan solo 3 pasos simples. En este artículo, te eplicaremos cómo identificar un ángulo obtuso en un triángulo de manera fácil y rápida.
Paso 1: Conocer los tipos de ángulos en un triángulo
Antes de comenzar a identificar un ángulo obtuso, es importante tener claridad sobre los diferentes tipos de ángulos que eisten en un triángulo. Un triángulo está compuesto por tres ángulos internos, cuya suma siempre es igual a 180 grados.
En función de la medida de estos ángulos, podemos clasificarlos en tres tipos: agudos, rectos u obtusos. Un ángulo obtuso es aquel cuya medida es mayor a 90 grados pero menor a 180 grados.
Paso 2: Medir los ángulos del triángulo
Una vez que tenemos claro qué es un ángulo obtuso, el siguiente paso es medir los ángulos del triángulo en cuestión. Esto puede hacerse utilizando una regla o transportador, asegurándonos de colocarlo adecuadamente en cada vértice para obtener medidas precisas.
Es importante medir los tres ángulos del triángulo y anotar sus respectivas medidas. Estas medidas serán fundamentales para determinar si alguno de los ángulos es obtuso o no.
Paso 3: Comparar las medidas de los ángulos
Una vez que tenemos las medidas de los ángulos del triángulo, es momento de analizarlos y compararlos entre sí. Si alguno de los tres ángulos tiene una medida mayor a 90 grados pero menor a 180 grados, entonces podemos afirmar que el triángulo tiene un ángulo obtuso.
Es importante recordar que si ninguno de los ángulos cumple con esta condición, entonces el triángulo no tiene ángulos obtusos, sino que puede tener ángulos agudos (menores a 90 grados) o rectos (iguales a 90 grados).
Recuerda que identificar los ángulos en un triángulo puede ser útil en diversas áreas, como la geometría o la resolución de problemas matemáticos. Ahora que conoces estos pasos sencillos, podrás identificar rápidamente si un triángulo tiene un ángulo obtuso o no. ¡Pon en práctica estos conocimientos y sigue eplorando el fascinante mundo de la geometría!
Cuál es la importancia de identificar los ángulos obtusos en un triángulo
Identificar los ángulos obtusos en un triángulo es de suma importancia en el campo de la geometría y las matemáticas en general. Los ángulos obtusos son aquellos cuya medida es mayor a 90 grados, lo que significa que se encuentran más abiertos que un ángulo recto. Estos ángulos pueden tener diversas aplicaciones prácticas, tanto en la vida cotidiana como en disciplinas más especializadas.
En primer lugar, conocer y comprender los ángulos obtusos en un triángulo es fundamental para resolver problemas de geometría euclidiana. Al identificar estos ángulos, podemos determinar la clasificación y características del triángulo en cuestión. Por ejemplo, si un triángulo tiene un ángulo obtuso, sabemos que no puede ser un triángulo equilátero ni un triángulo rectángulo, ya que éstos últimos tienen ángulos agudos y no obtusos.
Asimismo, la identificación de los ángulos obtusos nos permite analizar y describir las propiedades y relaciones entre los elementos del triángulo. En geometría, eisten diversas fórmulas y teoremas que se aplican específicamente a triángulos con ángulos obtusos. Por ejemplo, el teorema de las perpendiculares establece que en un triángulo con un ángulo obtuso, la altura trazada desde el vértice opuesto a ese ángulo eteriormente forma un ángulo agudo con el lado opuesto. Esta propiedad nos permite calcular medidas y relaciones adicionales dentro del triángulo, lo cual resulta invaluable en la resolución de problemas geométricos más complejos.
Por otro lado, el conocimiento de los ángulos obtusos en un triángulo también tiene aplicaciones más allá del mundo matemático. Por ejemplo, en arquitectura e ingeniería, comprender las propiedades y características de diferentes tipos de triángulos es esencial para llevar a cabo construcciones seguras y estables. La presencia de un ángulo obtuso puede indicar ciertas limitaciones o requisitos específicos en cuanto a la distribución de cargas o resistencia estructural.
Ejemplo de identificación de un ángulo obtuso en un triángulo
Supongamos que tenemos un triángulo ABC y queremos determinar si tiene algún ángulo obtuso. Para ello, podemos seguir los siguientes pasos:
- Medir los ángulos internos del triángulo utilizando un transportador o instrumento de medición adecuado.
- Comparar las medidas obtenidas con la definición de ángulo obtuso (mayor a 90 grados).
- Si encontramos algún ángulo cuya medida sea mayor a 90 grados, concluimos que el triángulo tiene al menos un ángulo obtuso.
Este proceso sencillo nos permite identificar rápidamente si un triángulo tiene ángulos obtusos. Es importante recordar que los ángulos obtusos pueden variar en medida desde ligeramente mayor a 90 grados hasta casi 180 grados, por lo que se requiere un análisis detallado y preciso para determinar su clasificación.
La identificación de los ángulos obtusos en un triángulo es esencial tanto en el campo de la geometría como en disciplinas relacionadas. Esta habilidad nos permite comprender las propiedades y relaciones dentro del triángulo, resolver problemas geométricos más complejos y aplicar ese conocimiento en diversas áreas prácticas. La próima vez que te encuentres con un triángulo, no olvides verificar si presenta algún ángulo obtuso y aprovecha toda la información valiosa que puedes obtener de él.
Cuáles son los diferentes tipos de triángulos y sus características
Los triángulos son polígonos que constan de tres lados y tres ángulos. Dependiendo de las longitudes de sus lados y las medidas de sus ángulos, los triángulos pueden clasificarse en diferentes tipos.
Triángulo equilátero
- Un triángulo equilátero tiene todos sus lados de la misma longitud.
- Todos sus ángulos también tienen la misma medida, que es de 60 grados.
- En un triángulo equilátero, todas las alturas, medianas y bisectrices son líneas coincidentes.
Triángulo isósceles
- Un triángulo isósceles tiene dos lados de la misma longitud y uno diferente.
- Los ángulos opuestos a los lados iguales también tienen la misma medida.
- El ángulo formado por los dos lados iguales se llama ángulo base, mientras que los otros dos ángulos se llaman ángulos cúspides o vértices.
Triángulo escaleno
- Un triángulo escaleno tiene todos sus lados de longitudes diferentes.
- Sus ángulos también tienen medidas diferentes.
- No hay ninguna relación especial entre los ángulos y los lados de un triángulo escaleno.
Triángulo rectángulo
- Un triángulo rectángulo tiene un ángulo recto, es decir, un ángulo de 90 grados.
- El lado opuesto al ángulo recto se llama hipotenusa, mientras que los otros dos lados se llaman catetos.
- La suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, según el teorema de Pitágoras.
Triángulo obtuso
- Un triángulo obtuso tiene un ángulo mayor a 90 grados.
- Los otros dos ángulos son agudos, es decir, menores a 90 grados.
- En un triángulo obtuso, el segmento más largo se encuentra opuesto al ángulo obtuso.
Estos son algunos de los diferentes tipos de triángulos y sus características. Ahora que tienes una mejor comprensión de ellos, ¡puedes poner en práctica tus conocimientos para identificar rápidamente qué triángulo tiene un ángulo obtuso en solo 3 pasos!
¡No te pierdas nuestro próimo artículo donde te enseñaremos cómo identificarlo!
Cómo se puede determinar si un triángulo tiene un ángulo obtuso en solo 3 pasos
Los triángulos son figuras geométricas que constan de tres lados y tres ángulos. Dependiendo de la medida de sus ángulos, los triángulos pueden clasificarse en diferentes tipos: equiláteros, isósceles, escalenos y rectángulos. Sin embargo, también eiste otro tipo particular de triángulo conocido como un triángulo obtuso.
Un triángulo obtuso es aquel que tiene un ángulo mayor a 90 grados. Esto significa que al menos uno de los ángulos internos del triángulo es mayor a un ángulo recto, lo cual le confiere una forma distinta y características particulares.
Ahora bien, ¿cómo podemos determinar si un triángulo tiene un ángulo obtuso en solo 3 pasos? A continuación, te presentamos una guía sencilla y práctica para realizar esta verificación de forma rápida y precisa:
Paso 1: Conoce las medidas de los ángulos internos
El primer paso para determinar si un triángulo tiene un ángulo obtuso es conocer las medidas de sus ángulos internos. Recuerda que la suma de los ángulos internos de un triángulo siempre es igual a 180 grados.
Así que, toma una regla o transportador y mide los ángulos internos del triángulo en cuestión. Anota las medidas obtenidas para cada ángulo, ya que serán necesarias en los siguientes pasos.
Paso 2: Identifica el ángulo más grande
Una vez que tienes las medidas de los ángulos internos, el siguiente paso consiste en identificar cuál de ellos es el más grande. Para ello, compara las medidas anotadas y busca aquel ángulo cuya medida sea mayor a 90 grados.
Recuerda que solo necesitas encontrar un ángulo mayor a 90 grados para confirmar que el triángulo tiene un ángulo obtuso. Si encuentras más de uno, es posible que el triángulo tenga más de un ángulo obtuso y se clasifique dentro de esta categoría particular.
Paso 3: Verifica si cumple con la condición
Una vez que has identificado el ángulo más grande del triángulo, el último paso consiste en verificar si cumple con la condición para ser considerado un triángulo obtuso. Recuerda que un triángulo obtuso debe tener al menos un ángulo mayor a 90 grados.
Si el ángulo identificado en el paso anterior cumple con esta condición, entonces puedes afirmar que el triángulo efectivamente tiene un ángulo obtuso. En cambio, si ninguno de los ángulos supera los 90 grados, entonces el triángulo no puede ser clasificado como obtuso.
Determinar si un triángulo tiene un ángulo obtuso en solo 3 pasos es realmente sencillo. Conociendo las medidas de los ángulos internos, identificando el ángulo más grande y verificando si cumple con la condición, podrás saber rápidamente si un triángulo es obtuso o no.
Cuál es el primer paso para identificar un ángulo obtuso en un triángulo
El primer paso para identificar un ángulo obtuso en un triángulo es comprender qué es un ángulo obtuso y cómo se puede reconocer. Un ángulo obtuso es aquel que mide más de 90 grados pero menos de 180 grados.
Para identificar si un triángulo tiene un ángulo obtuso, debemos eaminar cuidadosamente los ángulos del triángulo y comparar sus medidas con la definición de un ángulo obtuso. Eisten diferentes métodos para hacer esto, pero aquí te presentamos un sencillo proceso de 3 pasos para facilitar su identificación.
Paso 1: Medir los ángulos del triángulo
En este primer paso, debemos medir los tres ángulos del triángulo utilizando un transportador u otra herramienta de medición adecuada.
Coloca el transportador en uno de los vértices del triángulo y asegúrate de que la base del transportador esté alineada con uno de los lados del triángulo. Luego, lee la medida del ángulo indicada en el transportador.
Paso 2: Comparar las medidas de los ángulos con 90 grados
Una vez que hayas medido los tres ángulos del triángulo, compara las medidas obtenidas con el valor de 90 grados. Recuerda que un ángulo obtuso debe tener una medida mayor a 90 grados pero menor a 180 grados.
Si alguno de los tres ángulos tiene una medida mayor a 90 grados pero menor a 180 grados, entonces el triángulo tiene al menos un ángulo obtuso.
Paso 3: Identificar y marcar el ángulo obtuso
En este último paso, debemos identificar y marcar el ángulo obtuso en el triángulo. Utilizando las medidas de los ángulos obtenidas en el paso anterior, busca aquel que cumpla con la definición de un ángulo obtuso: mayor a 90 grados pero menor a 180 grados.
Una vez identificado el ángulo obtuso, puedes marcarlo con una letra o algún otro símbolo para facilitar su reconocimiento.
Ahora que conoces los 3 pasos para identificar un ángulo obtuso en un triángulo, estás listo para poner en práctica esta habilidad. Recuerda que la práctica es fundamental para mejorar tus habilidades matemáticas y geométricas.
Cuáles son las medidas de los ángulos en un triángulo rectángulo
En un triángulo rectángulo, uno de los ángulos es siempre recto, es decir, mide eactamente 90 grados. Los otros dos ángulos, llamados ángulos agudos, son aquellos que miden menos de 90 grados.
Para determinar las medidas de los ángulos en un triángulo rectángulo, podemos utilizar el teorema de Pitágoras y las funciones trigonométricas seno, coseno y tangente.
Teorema de Pitágoras
El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos. Matemáticamente, esto se epresa con la siguiente fórmula:
a^2 + b^2 = c^2
Donde "a" y "b" representan las longitudes de los catetos, y "c" representa la longitud de la hipotenusa.
Funciones trigonométricas
Las funciones trigonométricas son herramientas matemáticas que nos permiten relacionar las medidas de los ángulos en un triángulo rectángulo con las longitudes de sus lados. Las principales funciones trigonométricas utilizadas en triángulos rectángulos son el seno, el coseno y la tangente.
- El seno de un ángulo en un triángulo rectángulo se define como la razón entre la longitud del cateto opuesto a ese ángulo y la longitud de la hipotenusa.
- El coseno de un ángulo en un triángulo rectángulo se define como la razón entre la longitud del cateto adyacente a ese ángulo y la longitud de la hipotenusa.
- La tangente de un ángulo en un triángulo rectángulo se define como la razón entre la longitud del cateto opuesto a ese ángulo y la longitud del cateto adyacente.
Estas funciones nos permiten calcular las medidas de los ángulos en un triángulo rectángulo a partir de las longitudes de sus lados, o viceversa. Son ampliamente utilizadas en diversos campos de la ciencia y la ingeniería.
En un triángulo rectángulo uno de los ángulos es siempre recto (90 grados), mientras que los otros dos ángulos son agudos (menos de 90 grados). Además, podemos utilizar el teorema de Pitágoras y las funciones trigonométricas para relacionar las medidas de los ángulos con las longitudes de los lados de un triángulo rectángulo.
Cuál es el segundo paso para identificar un ángulo obtuso en un triángulo
Una vez que hemos identificado el triángulo y conocemos las medidas de sus ángulos, pasamos al siguiente paso para determinar si tiene un ángulo obtuso o no. Este segundo paso consiste en comparar cada uno de los ángulos con 90 grados, que es el valor correspondiente a un ángulo recto.
Para realizar esta comparación, podemos usar una herramienta muy útil llamada transportador. Colocamos el origen del transportador en el vértice del ángulo que queremos medir y trazamos una línea desde este punto hasta la marca de 90 grados del transportador. Luego, verificamos si el lado opuesto del ángulo cae dentro del rango de valores marcados en el transportador.
Si el lado opuesto del ángulo cae por encima de los 90 grados en el transportador, entonces ese ángulo será un ángulo obtuso. En cambio, si cae por debajo de los 90 grados, estaremos frente a un ángulo agudo. De esta manera, podemos identificar si el triángulo tiene un ángulo obtuso o no.
Es importante recordar que un ángulo obtuso se caracteriza por ser mayor que un ángulo recto (90 grados) pero menor que un ángulo llano (180 grados). Por lo tanto, al comparar los ángulos con 90 grados podemos determinar si alguno de ellos cumple con esta característica particular.
El segundo paso para identificar un ángulo obtuso en un triángulo es comparar cada ángulo con 90 grados usando un transportador. Si el lado opuesto del ángulo cae por encima de los 90 grados en el transportador, estaremos frente a un ángulo obtuso. Por el contrario, si cae por debajo de los 90 grados, tendremos un ángulo agudo. Este método nos permite determinar con precisión si el triángulo tiene un ángulo obtuso y continuar con el tercer paso para completar la identificación.
Qué es un triángulo equilátero y cómo se relaciona con los ángulos
Un triángulo equilátero es aquel que tiene todos sus lados y ángulos iguales. Es esencialmente un caso especial de triángulo donde las tres longitudes de los lados son iguales. Esto significa que cada ángulo interno en un triángulo equilátero mide eactamente 60 grados.
El hecho de que un triángulo equilátero tenga sus ángulos internos iguales a 60 grados es una propiedad notoria y útil. Esta característica se basa en el concepto de la suma de los ángulos internos de un triángulo, que siempre es igual a 180 grados. En el caso particular del triángulo equilátero, como los tres ángulos internos son iguales, cada uno debe ser igual a 60 grados para que la suma total sea 180 grados.
Además de su relación con los ángulos, el triángulo equilátero también tiene propiedades interesantes en términos de simetría. Debido a que todos los lados y ángulos son iguales, un triángulo equilátero es simétrico alrededor de su centro. Esto significa que si trazamos una línea vertical desde el vértice superior del triángulo hasta la base, dividirá el triángulo en dos partes eactamente iguales.
Usando la figura geométrica del triángulo equilátero para identificar ángulos obtusos
Una vez que entendemos qué es un triángulo equilátero y cómo se relaciona con los ángulos, podemos utilizar esta figura geométrica para identificar triángulos que tienen un ángulo obtuso.
Recordemos que un ángulo obtuso es aquel cuya medida es mayor a 90 grados pero menor a 180 grados. Para identificar un triángulo con un ángulo obtuso, primero debemos observar si algún ángulo interno del triángulo equilátero ecede los 90 grados.
Si encontramos un ángulo en el triángulo equilátero mayor a 90 grados, podemos concluir que ese triángulo tiene al menos un ángulo obtuso. Sin embargo, si todos los ángulos internos del triángulo son menores o iguales a 90 grados, podemos afirmar que no hay ángulos obtusos presentes en ese triángulo.
El concepto del triángulo equilátero nos proporciona una herramienta visual y conceptualmente simple para identificar si un triángulo tiene ángulos obtusos. Observando los ángulos internos de la figura y evaluando si alguno supera los 90 grados, podemos determinar rápidamente si un triángulo en particular tiene un ángulo obtuso o no.
Cuál es el tercer paso para identificar un ángulo obtuso en un triángulo
Para identificar un ángulo obtuso en un triángulo, es importante seguir tres pasos claros y sencillos. El tercer paso en este proceso implica analizar cuidadosamente las medidas de los ángulos en el triángulo y determinar si alguno de ellos cumple con la condición para ser considerado como un ángulo obtuso.
Un ángulo obtuso se caracteriza por tener una medida mayor a 90 grados pero menor a 180 grados. En otras palabras, su apertura es más grande que un ángulo recto pero no alcanza la medida de un ángulo llano.
Para llevar a cabo este análisis, puedes valerte de diferentes métodos, dependiendo de las herramientas o conocimientos que tengas a tu disposición. A continuación, te presentamos algunas formas de identificar un ángulo obtuso en un triángulo:
1. Utilizando la medida de los ángulos
Si conoces las medidas eactas de los ángulos en el triángulo, puedes simplemente compararlas y determinar si alguna de ellas sobrepasa los 90 grados sin llegar a los 180 grados. En caso afirmativo, estarás frente a un ángulo obtuso.
Recuerda que la suma de los ángulos internos de cualquier triángulo siempre es igual a 180 grados. Por lo tanto, si ya conoces las medidas de dos ángulos del triángulo, puedes restar sus sumas a 180 para obtener la medida del tercer ángulo. Si este valor supera los 90 grados, entonces tienes un ángulo obtuso.
2. Utilizando la relación entre ángulos y lados
Otra forma de identificar un ángulo obtuso en un triángulo es analizando la relación entre los ángulos y los lados del triángulo. Si conoces las longitudes de los lados, puedes aplicar teoremas o propiedades geométricas para determinar si algún ángulo cumple con la condición de ser obtuso.
Por ejemplo, el Teorema del Coseno establece que en cualquier triángulo la siguiente ecuación es verdadera:
a² = b² + c² - 2bc * cos(A)
donde "a", "b" y "c" son las longitudes de los lados del triángulo y "A" es el ángulo opuesto al lado de longitud "a". Si el resultado de calcular el coseno y aplicar la fórmula resulta en un valor menor a cero, entonces estaremos frente a un ángulo obtuso.
3. Utilizando herramientas de dibujo o software
Si cuentas con herramientas como una regla, un transportador de ángulos, o software especializado en geometría, puedes utilizarlos para medir y analizar los ángulos en el triángulo. Estos dispositivos o programas suelen facilitar la tarea al proporcionarte medidas precisas y gráficos visuales que te permiten identificar rápidamente un ángulo obtuso.
También puedes utilizar software gratuito en línea que te permite dibujar triángulos y obtener información visual y métrica sobre ellos. Estas herramientas son especialmente útiles si deseas practicar o eperimentar con diferentes triángulos y ángulos obtusos.
El tercer paso para identificar un ángulo obtuso en un triángulo consiste en analizar las medidas de los ángulos, ya sea comparándolas directamente, aplicando teoremas o utilizando herramientas de dibujo y software especializado. Este paso es fundamental para determinar si un triángulo contiene un ángulo obtuso.
Cuáles son algunos ejemplos de triángulos que tienen un ángulo obtuso
En este artículo, te mostraremos algunos ejemplos de triángulos que tienen al menos un ángulo obtuso. Pero antes de adentrarnos en los diferentes tipos de triángulos, es importante comprender qué es eactamente un ángulo obtuso.
¿Qué es un ángulo obtuso?
Un ángulo obtuso es aquel cuya medida es mayor a 90 grados pero menor a 180 grados. En otras palabras, es un ángulo que es más abierto que un ángulo recto (90 grados) pero más cerrado que un ángulo llano (180 grados).
Ahora que tenemos claro qué es un ángulo obtuso, echemos un vistazo a algunos ejemplos de triángulos que contienen uno:
- Triángulo obtusángulo: Este tipo de triángulo tiene un ángulo obtuso. También cuenta con otros dos ángulos agudos, es decir, ángulos menores a 90 grados.
- Triángulo escaleno: Un triángulo escaleno puede tener uno o incluso todos sus ángulos obtusos.
- Triángulo isósceles: Aunque los triángulos isósceles por lo general tienen ángulos agudos, también eiste la posibilidad de que tengan un ángulo obtuso junto a dos ángulos iguales y agudos.
- Triángulo rectángulo: Si bien el ángulo recto en un triángulo rectángulo no es obtuso, los otros dos ángulos siempre suman 90 grados, dejando la posibilidad de que uno de ellos sea obtuso.
Recuerda que estos son solo algunos ejemplos y que eisten muchas otras combinaciones de longitudes de lados y medidas de ángulos en los triángulos que pueden resultar en ángulos obtusos.
Cómo identificar un ángulo obtuso en un triángulo en solo 3 pasos
Ahora que sabes qué es un ángulo obtuso y estás familiarizado con algunos ejemplos de triángulos que lo contienen, te mostraremos cómo identificar un ángulo obtuso en un triángulo en tan solo 3 pasos:
- Step 1: Eamina los ángulos del triángulo. Determina si alguno es mayor a 90 grados pero menor a 180 grados.
- Step 2: Si encuentras un ángulo que cumple con la descripción anterior, ese será el ángulo obtuso.
- Step 3: Verifica que la suma de los tres ángulos del triángulo sea igual a 180 grados. Si lo es, entonces se trata de un triángulo válido.
Siguiendo estos tres simples pasos, podrás identificar rápidamente si un triángulo tiene un ángulo obtuso o no.
Los triángulos que tienen al menos un ángulo obtuso son bastante comunes y se pueden encontrar en diferentes tipos de triángulos, como el obtusángulo, el escaleno, el isósceles y el rectángulo. Con solo seguir tres pasos simples, podrás identificar rápidamente si un triángulo tiene un ángulo obtuso o no. ¡Así que ponte a prueba y encuentra triángulos con ángulos obtusos!
Por qué es importante entender los ángulos obtusos en la geometría
En la geometría, uno de los conceptos clave que debemos comprender son los ángulos obtusos. Estos juegan un papel fundamental en la resolución de problemas geométricos y nos permiten clasificar los triángulos según sus características. Por lo tanto, entender qué es un ángulo obtuso y cómo identificarlo es crucial para cualquier estudiante o entusiasta de las matemáticas.
Un ángulo obtuso se define como aquel cuya medida es mayor a 90 grados pero menor a 180 grados. En otras palabras, es un ángulo que está abierto en una posición más grande que un ángulo recto pero aún se encuentra contenido dentro de un ángulo llano. Esto significa que el vértice del ángulo se ubica en el interior del triángulo y no en su eterior.
Para identificar si un triángulo tiene un ángulo obtuso, podemos seguir un proceso sencillo en tan solo tres pasos:
Paso 1: Obtén las medidas de todos los ángulos del triángulo
El primer paso consiste en obtener las medidas de cada uno de los ángulos del triángulo. Como recordatorio, la suma de los ángulos de cualquier triángulo siempre será igual a 180 grados. Por lo tanto, deberás conocer al menos dos de las medidas de los ángulos para poder determinar si hay algún ángulo obtuso presente.
Puedes usar instrumentos de medición como un transportador o simplemente leer las medidas de los ángulos si te las dan en el problema. Anota estas medidas para poder referirte a ellas en los próimos pasos.
Paso 2: Calcula la suma de las medidas de los ángulos del triángulo
Una vez que tengas las medidas de los ángulos, suma todas ellas para obtener la suma total. Nuevamente, recuerda que esta suma debe ser igual a 180 grados. Si la suma es mayor a 180 grados, verifica que hayas anotado correctamente las medidas de los ángulos o revisa si cometiste algún error en los cálculos. Si la suma es menor a 180 grados, deberás comprobar si hay algún defecto en tus mediciones o cálculos.
Paso 3: Identifica si alguno de los ángulos tiene medida mayor a 90 grados
En este último paso, eamina cada una de las medidas de los ángulos y busca si hay algún ángulo obtuso presente. Un ángulo será considerado obtuso si su medida es mayor a 90 grados. Si encuentras al menos un ángulo con esta característica, habrás identificado que el triángulo tiene un ángulo obtuso.
Los ángulos obtusos son fundamentales para entender y clasificar los triángulos según sus características. Siguiendo estos tres simples pasos, podrás determinar si un triángulo tiene o no un ángulo obtuso. ¡Así que no dudes en utilizar esta información la próima vez que te enfrentes a problemas geométricos o quieras impresionar a tus amigos con tus conocimientos matemáticos!
Cómo se pueden utilizar los ángulos obtusos en aplicaciones del mundo real
Los ángulos obtusos son un concepto matemático básico que se utiliza en muchas aplicaciones del mundo real. Estos ángulos, con una medida mayor a 90 grados pero menor a 180 grados, nos permiten entender y describir diversas situaciones y fenómenos en nuestro entorno.
1. Arquitectura y diseño
En el campo de la arquitectura y el diseño, los ángulos obtusos son fundamentales para crear estructuras sólidas y estéticamente agradables. Por ejemplo, al diseñar una casa, se pueden utilizar ángulos obtusos en las esquinas para generar un aspecto más moderno y único. Además, estos ángulos también pueden ayudar a optimizar el uso del espacio, permitiendo la incorporación de elementos adicionales.
2. Ingeniería civil
En la ingeniería civil, los ángulos obtusos son esenciales para el diseño de puentes y túneles. Estos elementos estructurales requieren una cuidadosa planificación y cálculos precisos de los ángulos, incluyendo los obtusos, para garantizar la seguridad y la resistencia de las construcciones. Además, los ángulos obtusos también pueden ser utilizados para la creación de rampas o inclinaciones suaves en carreteras y calles, facilitando el tráfico vehicular.
3. Geometría y trigonometría
Como es de esperarse, los ángulos obtusos tienen un papel fundamental en el estudio de la geometría y la trigonometría. Estos ángulos son clave para entender las relaciones entre los diversos elementos geométricos, como los triángulos y los polígonos. Además, en la trigonometría, los ángulos obtusos forman parte de las funciones trigonométricas inversas, como el coseno inverso y el tangente inversa.
Los ángulos obtusos son un concepto matemático que trasciende más allá del aula de clases. Su aplicación en el mundo real es variada y se puede encontrar en disciplinas como la arquitectura, el diseño, la ingeniería civil, la geometría y la trigonometría. A través de su comprensión y utilización adecuada, podemos dar forma a nuestro entorno de maneras sorprendentes e innovadoras.
Preguntas frecuentes (FAQ)
1. ¿Qué es un ángulo obtuso?
Un ángulo obtuso es aquel cuya medida es mayor a 90 grados y menor a 180 grados.
2. ¿Cuántos tipos de triángulos eisten?
Eisten varios tipos de triángulos, como el equilátero (todos los lados iguales), isósceles (dos lados iguales) y escaleno (ningún lado igual).
3. ¿Cómo puedo identificar un ángulo obtuso en un triángulo?
Para identificar si un triángulo tiene un ángulo obtuso, debes medir los tres ángulos interiores del triángulo utilizando un transportador. Si encuentras un ángulo que mida entre 90 y 180 grados, ese será un ángulo obtuso.
4. ¿Puede un triángulo tener más de un ángulo obtuso?
No, un triángulo solo puede tener máimo un ángulo obtuso. Los otros dos ángulos siempre serán agudos (menores a 90 grados) o rectos (de 90 grados).
5. ¿Se pueden encontrar ejemplos de triángulos con ángulo obtuso en la vida diaria?
Sí, se pueden encontrar ejemplos de triángulos con ángulo obtuso en muchas estructuras, como techos inclinados, rampas, pendientes de carreteras, entre otros.

Entradas relacionadas