Descubre cómo sacar el cateto de un triángulo rectángulo de forma rápida y sencilla

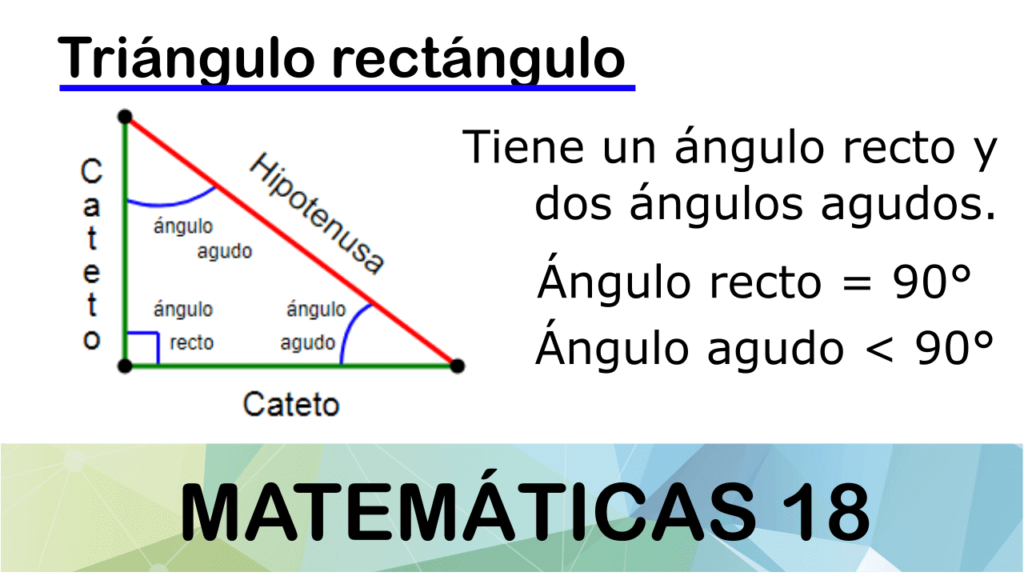
En la geometría, uno de los conceptos fundamentales es el triángulo rectángulo, que tiene un ángulo recto de 90 grados. Este tipo de triángulo es muy utilizado en problemas de trigonometría y cálculo de distancias, por lo que conocer sus propiedades y fórmulas es esencial.

En este artículo aprenderás una de las formas más sencillas y rápidas de calcular la longitud de uno de los catetos de un triángulo rectángulo cuando conoces la medida del otro cateto y la hipotenusa. Utilizando el teorema de Pitágoras y algunas operaciones matemáticas básicas, podrás resolver este tipo de problemas de manera eficiente.

Cuáles son las características de un triángulo rectángulo

Un triángulo rectángulo es un tipo especial de triángulo que cuenta con un ángulo recto, es decir, un ángulo de 90 grados. Esta característica particular hace que se pueda aprovechar para resolver problemas matemáticos y aplicaciones prácticas en diferentes áreas como la trigonometría, la geometría y la física.

Una de las características principales de un triángulo rectángulo es que está conformado por tres lados: dos catetos y una hipotenusa. Los catetos son los dos lados que forman el ángulo recto, mientras que la hipotenusa es el lado opuesto al ángulo recto.

Fórmula para encontrar la medida de un cateto en un triángulo rectángulo

Calcular la longitud de los catetos en un triángulo rectángulo puede resultar útil en muchas situaciones. Una fórmula comúnmente utilizada para encontrar la medida de un cateto se basa en el teorema de Pitágoras.

a² + b² = c²

Donde "a" y "b" representan las longitudes de los catetos, y "c" representa la longitud de la hipotenusa.

Para hallar la longitud de un cateto, solo es necesario tener la medida de la hipotenusa y la longitud del otro cateto. Por ejemplo, si conocemos la longitud de la hipotenusa y uno de los catetos, podemos resolver la ecuación y despejar el valor del otro cateto.

Ejemplo práctico de cómo sacar el cateto de un triángulo rectángulo

Supongamos que tenemos un triángulo rectángulo con una hipotenusa de longitud 10 cm y uno de los catetos mide 6 cm. Aplicando la fórmula de Pitágoras, podemos encontrar la longitud del otro cateto.

a² + b² = c²

Sustituyendo los valores conocidos:

6² + b² = 10²

Simplificando la ecuación:

36 + b² = 100

Restando 36 a ambos lados:

b² = 64

Finalmente, calculando la raíz cuadrada de ambos lados para despejar "b":

b = √64 = 8

Por lo tanto, el otro cateto del triángulo rectángulo tiene una longitud de 8 cm.

Utilidad y aplicaciones del cálculo de los catetos en un triángulo rectángulo

Saber cómo sacar el cateto de un triángulo rectángulo puede resultar de gran utilidad en diferentes contetos. En geometría, se puede utilizar para determinar longitudes desconocidas, encontrar ángulos y resolver problemas relacionados con la posición relativa de objetos en el espacio.

En trigonometría, el cálculo de los catetos es fundamental para realizar funciones trigonométricas como el seno, el coseno y la tangente. Estas funciones son ampliamente utilizadas en campos como la navegación marítima, la ingeniería civil y la física.

Además, el conocimiento de cómo sacar el cateto de un triángulo rectángulo también puede ser aplicado en problemas prácticos del día a día, como calcular distancias, alturas o pendientes en diferentes situaciones.

Saber cómo sacar el cateto de un triángulo rectángulo es una habilidad matemática fundamental que tiene múltiples aplicaciones tanto en el ámbito teórico como en la vida cotidiana. La fórmula de Pitágoras y las propiedades de los triángulos rectángulos permiten resolver estos cálculos de forma rápida y sencilla, brindando herramientas útiles para resolver problemas geométricos y aplicaciones prácticas en diversas disciplinas.

Qué es un cateto en un triángulo rectángulo

En un triángulo rectángulo, los catetos son los dos lados que forman el ángulo recto. Son opuestos al ángulo recto y se encuentran adyacentes a él. Conocer los catetos de un triángulo rectángulo es fundamental para poder calcular la longitud de los otros elementos del triángulo, como la hipotenusa o los ángulos.

La importancia de sacar el cateto de un triángulo rectángulo radica en que es una operación muy común en diversos campos de la ciencia y la ingeniería, ya que permite resolver problemas de geometría y trigonometría. Además, el cálculo de los catetos puede ser útil en situaciones cotidianas, como determinar la altura de un edificio o la longitud de un terreno.

Métodos para sacar el cateto de un triángulo rectángulo

Eisten diferentes métodos para calcular los catetos de un triángulo rectángulo, dependiendo de la información de la que se disponga. Uno de los métodos más conocidos es el teorema de Pitágoras, que establece que en un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

Otro método muy utilizado es la trigonometría. A través de las funciones trigonométricas seno, coseno y tangente, es posible determinar las longitudes de los catetos a partir de los ángulos y la hipotenusa.

Además, también se pueden utilizar fórmulas específicas para calcular los catetos en casos particulares, como el teorema de Euclides o las relaciones trigonométricas en triángulos rectángulos especiales.

Consejos para sacar el cateto de un triángulo rectángulo

Al momento de calcular los catetos de un triángulo rectángulo, es importante tener en cuenta algunos consejos que te ayudarán a realizar los cálculos de forma correcta y precisa:

• Verificar si se dispone de suficiente información: antes de intentar calcular los catetos, es necesario asegurarse de contar con todos los datos necesarios, como la medida de los ángulos o la hipotenusa.
• Utilizar unidades consistentes: al trabajar con medidas, es fundamental utilizar siempre las mismas unidades para evitar errores en los cálculos.
• Aplicar correctamente las fórmulas o teoremas: es fundamental comprender el método que se va a utilizar y aplicarlo adecuadamente, teniendo en cuenta las condiciones del triángulo rectángulo.
• Revisar los resultados obtenidos: una vez realizados los cálculos, es recomendable revisar los resultados para detectar posibles errores y corregirlos si es necesario.

Siguiendo estos consejos y utilizando los métodos adecuados, podrás sacar el cateto de un triángulo rectángulo de forma rápida y sencilla, permitiéndote resolver problemas matemáticos y geométricos con facilidad.

Por qué es importante sacar el cateto de un triángulo rectángulo

Cuando se trabaja con triángulos rectángulos, es crucial poder sacar el cateto de forma rápida y sencilla. Esto se debe a que el cateto es uno de los lados más importantes de este tipo de triángulo, ya que forma el ángulo recto y está directamente relacionado con los otros dos lados, la hipotenusa y el otro cateto.

Saber cómo sacar el cateto no solo es fundamental en matemáticas, donde se utilizan constantemente los triángulos rectángulos para resolver problemas geométricos, sino también en muchas otras áreas de la vida cotidiana. La arquitectura, la ingeniería, la navegación y la física son solo algunas de las disciplinas que requieren un conocimiento sólido de los triángulos rectángulos y su cálculo.

La fórmula del teorema de Pitágoras

Una de las formas más comunes de sacar el cateto de un triángulo rectángulo es utilizando el teorema de Pitágoras. Este famoso teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

a^2 + b^2 = c^2

Donde 'a' y 'b' representan los catetos, y 'c' corresponde a la hipotenusa.

Usando esta fórmula, podemos despejar el valor de uno de los catetos si conocemos la longitud de la hipotenusa y el otro cateto. Supongamos que sabemos la longitud de la hipotenusa y uno de los catetos:

Si conocemos 'c' (hipotenusa) y 'a' (cateto), podemos sustituir esos valores en la fórmula:

a^2 + b^2 = c^2
a^2 + b^2 = c^2
b^2 = c^2 - a^2
b = √(c^2 - a^2)

De esta manera, podemos obtener el valor del cateto 'b'.

Utilizando las razones trigonométricas

Otra forma de sacar el cateto de un triángulo rectángulo es utilizando las razones trigonométricas, como el seno, el coseno y la tangente.

Para sacar un cateto usando estas razones, primero debemos identificar qué cateto estamos buscando y qué ratios tenemos disponibles.

Por ejemplo, si queremos encontrar el valor de 'a', el cateto opuesto al ángulo agudo, y conocemos el valor de un ángulo y la hipotenusa, podemos utilizar el seno:

sen(a) = a / c
a = sen(a) * c

De manera similar, si queremos encontrar el valor de 'a' y conocemos el valor de un ángulo y el cateto adyacente, podemos utilizar el coseno:

cos(a) = a / c
a = cos(a) * c

Si queremos encontrar el valor de 'a' y conocemos el cateto adyacente y el cateto opuesto, podemos utilizar la tangente:

tan(a) = a / b
a = tan(a) * b

Utilizando estas razones trigonométricas, podemos sacar el cateto de forma rápida y sencilla, siempre y cuando tengamos los valores adecuados.

Sacar el cateto de un triángulo rectángulo es fundamental en matemáticas y en muchas otras áreas de estudio y profesiones. La fórmula del teorema de Pitágoras y las razones trigonométricas son herramientas valiosas que nos permiten calcular el valor de un cateto de manera eficiente. Conocer estas técnicas nos ayudará a resolver problemas geométricos y aplicar el cálculo en situaciones prácticas de nuestra vida diaria.

Cuál es la fórmula para calcular la longitud de un cateto en un triángulo rectángulo

Para calcular la longitud de un cateto en un triángulo rectángulo podemos utilizar el famoso teorema de Pitágoras. Este teorema establece que en un triángulo rectángulo, la suma de los cuadrados de las longitudes de los dos catetos es igual al cuadrado de la longitud de la hipotenusa.

La fórmula para calcular la longitud de un cateto es la siguiente:

cateto = √(hipotenusa^2 - otro_cateto^2)

Donde "cateto" representa la longitud que deseamos calcular, "hipotenusa" es la longitud de la hipotenusa del triángulo rectángulo y "otro_cateto" es la longitud del cateto conocido.

Ejemplo práctico

Supongamos que tenemos un triángulo rectángulo con una hipotenusa de longitud 10 unidades y un cateto conocido de longitud 6 unidades. Utilizando la fórmula mencionada anteriormente, podemos calcular el valor del cateto desconocido de la siguiente manera:

cateto = √(10^2 - 6^2)
cateto = √(100 - 36)
cateto = √64
cateto = 8 unidades

Por lo tanto, en este ejemplo, el cateto desconocido tiene una longitud de 8 unidades.

Es importante recordar que esta fórmula solo se aplica a triángulos rectángulos, es decir, aquellos triángulos que tienen un ángulo recto (90 grados). En otros tipos de triángulos, como los triángulos equiláteros o isósceles, la longitud de los catetos se calcula de manera diferente.

Así que la próima vez que te encuentres con un triángulo rectángulo y necesites calcular la longitud de un cateto, recuerda utilizar el teorema de Pitágoras y esta sencilla fórmula. ¡Verás lo fácil que es resolver este tipo de problemas!

Puedes eplicar paso a paso cómo sacar el cateto de un triángulo rectángulo

Los triángulos rectángulos son una figura geométrica muy común en matemáticas y física. Su característica principal es tener un ángulo recto, es decir, de 90 grados. Una de las operaciones básicas que podemos realizar con triángulos rectángulos es calcular sus lados, especialmente los catetos.

¿Qué es un cateto?

Antes de entrar en cómo sacar el cateto de un triángulo rectángulo, es importante entender qué es un cateto. En un triángulo rectángulo, los catetos son los dos lados que forman el ángulo recto, es decir, los lados que no corresponden a la hipotenusa. Uno de los catetos se denomina cateto adyacente y el otro cateto opuesto.

Método para sacar el cateto adyacente

Para sacar el cateto adyacente de un triángulo rectángulo, necesitaremos conocer el valor del ángulo opuesto al cateto que queremos hallar y la longitud de la hipotenusa. Si tenemos estos datos, podemos utilizar la función trigonométrica del coseno para obtener el valor del cateto adyacente.


cateto_adyacente = hipotenusa * cos(angulo_opuesto)


Donde:

• cateto_adyacente: Longitud del cateto adyacente.
• hipotenusa: Longitud de la hipotenusa.
• angulo_opuesto: Valor del ángulo opuesto al cateto adyacente en radianes.

Es importante asegurarse de que los valores estén en las mismas unidades (por ejemplo, ambos en cm o ambos en m) antes de realizar el cálculo. Una vez realizada la operación, obtendremos la longitud del cateto adyacente.

Método para sacar el cateto opuesto

Por otro lado, si deseamos calcular el cateto opuesto de un triángulo rectángulo, necesitaremos conocer el valor del ángulo adyacente al cateto que queremos hallar y la longitud de la hipotenusa. En este caso, utilizaremos la función trigonométrica del seno.


cateto_opuesto = hipotenusa * sin(angulo_adyacente)


Donde:

• cateto_opuesto: Longitud del cateto opuesto.
• hipotenusa: Longitud de la hipotenusa.
• angulo_adyacente: Valor del ángulo adyacente al cateto opuesto en radianes.

Al igual que en el caso del cateto adyacente, es fundamental que los valores estén en las mismas unidades antes de realizar el cálculo. Una vez aplicada la fórmula, obtendremos la longitud del cateto opuesto.

Calcular los catetos de un triángulo rectángulo puede parecer complicado al principio, pero con el uso de las funciones trigonométricas adecuadas, podemos obtener estos valores de manera rápida y sencilla. Ya sea el cateto adyacente o el cateto opuesto, solo necesitamos conocer la longitud de la hipotenusa y el ángulo correspondiente para aplicar la fórmula correspondiente.

Recuerda que practicar estos ejercicios te ayudará a familiarizarte con los conceptos matemáticos y a entender mejor la geometría y la trigonometría.

¿Cuáles son algunos ejemplos prácticos de cómo utilizar esta fórmula?

Una de las aplicaciones más comunes para sacar el cateto de un triángulo rectángulo es en problemas de trigonometría. Por ejemplo, supongamos que tenemos un poste vertical de 10 metros de altura y queremos calcular la longitud de la sombra que proyecta en el suelo utilizando un ángulo dado.

Para resolver este problema, podemos utilizar la fórmula del cateto de un triángulo rectángulo. En este caso, conocemos la altura del poste, que actúa como la hipotenusa del triángulo rectángulo, y el ángulo entre la hipotenusa y el cateto desconocido.

Podemos proceder de la siguiente manera:

1. Primero, convertimos el ángulo dado a radianes si es necesario.
2. Luego, utilizando la función trigonométrica seno (sen), podemos establecer la relación entre el cateto desconocido, la hipotenusa y el ángulo:

sin(ángulo) = cateto / hipotenusa

3. Despejamos el valor del cateto desconocido:

cateto = sen(ángulo) * hipotenusa

Aplicando esta fórmula al problema mencionado, si el ángulo es de 30 grados, podemos calcular lo siguiente:

cateto = sen(30°) * 10 m

Simplificando la ecuación:

cateto = 0.5 * 10 m
cateto = 5 m

Por lo tanto, la longitud de la sombra proyectada por el poste vertical de 10 metros de altura bajo un ángulo de 30 grados es de 5 metros.

Otro ejemplo práctico de cómo utilizar esta fórmula es en problemas de navegación marítima. Supongamos que estamos navegando y queremos determinar la distancia a la costa utilizando un ángulo y la altura de nuestro punto de observación.

En este caso, podemos aplicar la misma fórmula del cateto:

1. Convertimos el ángulo a radianes si es necesario.
2. Utilizando la función seno (sen), establecemos la relación entre el cateto desconocido, la hipotenusa (distancia a la costa) y el ángulo.
3. Despejamos el valor del cateto desconocido.

Utilizando esta fórmula, podemos estimar la distancia a la costa basándonos en la altura del punto de observación y el ángulo dado.

Estos son solo dos ejemplos de cómo sacar el cateto de un triángulo rectángulo de forma rápida y sencilla utilizando esta fórmula. La trigonometría y la navegación marítima son solo algunas áreas donde esta fórmula es fundamental para realizar cálculos precisos y eficientes.

Eisten otras formas de calcular la longitud de un cateto en un triángulo rectángulo

Calcular la longitud de un cateto en un triángulo rectángulo es una tarea fundamental en geometría. Eisten varias fórmulas y métodos para realizar este cálculo, pero algunos pueden resultar complicados y requieren de conocimientos matemáticos avanzados. Sin embargo, eiste una forma rápida y sencilla de obtener esta medida utilizando el teorema de Pitágoras.

El teorema de Pitágoras

El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los catetos (los otros dos lados). Matemáticamente se epresa de la siguiente manera:

a^2 + b^2 = c^2

donde "a" y "b" representan las longitudes de los catetos, y "c" representa la longitud de la hipotenusa.

Si deseamos calcular la longitud de uno de los catetos, podemos despejar su valor de la ecuación del teorema de Pitágoras. Para ello, supongamos que queremos encontrar la longitud del cateto "a", entonces la ecuación sería:

a^2 = c^2 - b^2

Para encontrar el valor de "a", simplemente debemos etraer la raíz cuadrada de ambos lados de la ecuación:

a = √(c^2 - b^2)

De esta manera, hemos obtenido una fórmula sencilla y eficiente para calcular la longitud de un cateto en un triángulo rectángulo. Basta con conocer la longitud de la hipotenusa y la del otro cateto para poder aplicarlo.

Ejemplo práctico

Supongamos que tenemos un triángulo rectángulo donde la hipotenusa mide 5 unidades y el otro cateto mide 3 unidades. Aplicando la fórmula que derivamos anteriormente, podemos calcular la longitud del cateto restante:

a = √(c^2 - b^2)
a = √(5^2 - 3^2)
a = √(25 - 9)
a = √16
a = 4

Por lo tanto, la longitud del cateto desconocido en este ejemplo es de 4 unidades.

Calcular la longitud de un cateto en un triángulo rectángulo puede parecer complicado al principio, pero utilizando el teorema de Pitágoras podemos realizar este cálculo de manera rápdia y sencilla. Al seguir los pasos mencionados anteriormente, podemos obtener el resultado sin necesidad de tener conocimientos matemáticos avanzados. Este teorema es una herramienta fundamental en geometría y puede ser utilizado en diversos problemas y situaciones que involucren triángulos rectángulos.

Preguntas frecuentes (FAQ)

1. ¿Qué es un cateto en un triángulo rectángulo?

Un cateto en un triángulo rectángulo es uno de los dos lados que forman el ángulo recto.

2. ¿Cómo se puede calcular la longitud de un cateto?

Para calcular la longitud de un cateto en un triángulo rectángulo puedes usar el teorema de Pitágoras o aplicar las razones trigonométricas según los datos proporcionados.

3. ¿Cuál es la función del cateto en un triángulo rectángulo?

El cateto en un triángulo rectángulo sirve para formar el ángulo recto y permite calcular la longitud de los otros lados del triángulo mediante diferentes fórmulas y teoremas.

4. ¿Cuál es la diferencia entre el cateto opuesto y el cateto adyacente?

El cateto opuesto es aquel que no está junto al ángulo en cuestión, mientras que el cateto adyacente es aquel que está justo al lado del ángulo.

5. ¿Qué sucede si se desconoce la longitud de ambos catetos?

Si se desconoce la longitud de ambos catetos, es necesario contar con otro dato como la hipotenusa o algún ángulo conocido para poder resolver el triángulo rectángulo utilizando las herramientas matemáticas disponibles.