Descubre cómo calcular el área de una figura geométrica de forma sencilla y precisa

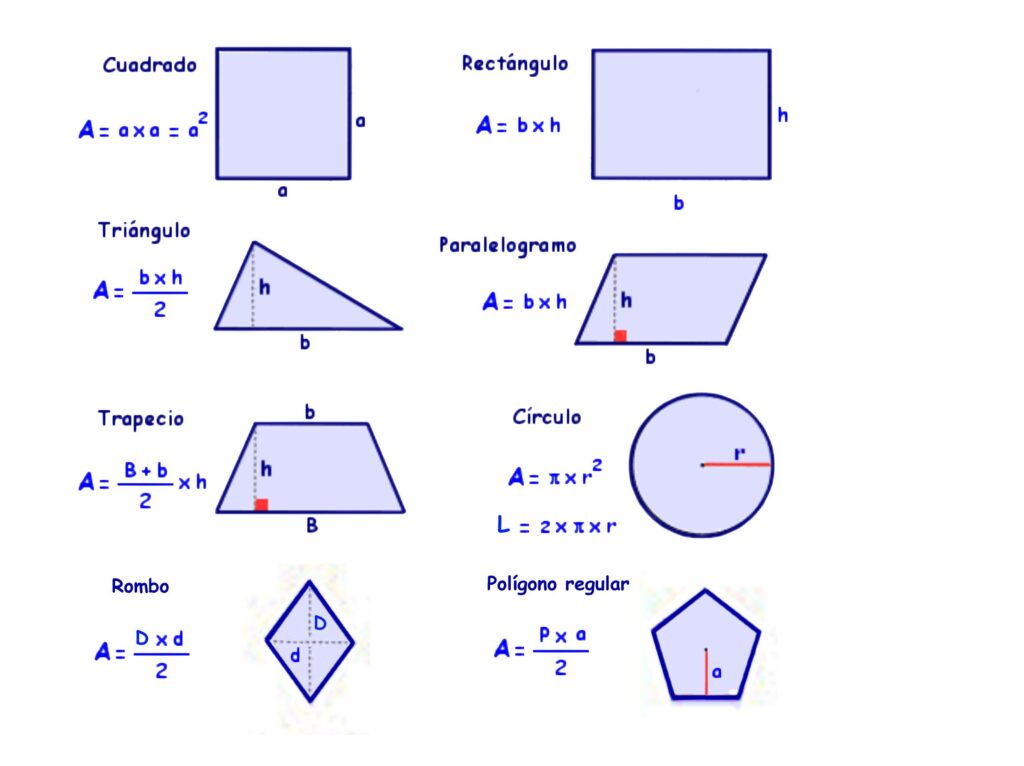
El cálculo del área de una figura geométrica es un concepto fundamental dentro de la geometría. Nos permite determinar la cantidad de espacio que ocupa una figura en un plano o en el espacio tridimensional. Este conocimiento es utilizado en diversas áreas como la ingeniería, la arquitectura, la física y las matemáticas.

Te mostraremos cómo calcular el área de diferentes figuras geométricas de forma sencilla y precisa. Eplicaremos los métodos más comunes utilizados para calcular el área de triángulos, cuadrados, rectángulos, círculos y trapecios, brindándote fórmulas y ejemplos paso a paso. Además, te daremos algunos consejos y recordatorios útiles que te ayudarán a realizar estos cálculos con facilidad. Al finalizar, tendrás todas las herramientas necesarias para resolver problemas relacionados con el área de figuras geométricas de manera eficiente y precisa.

Cuáles son las fórmulas básicas para calcular el área de un triángulo

El triángulo es una de las figuras geométricas más básicas y también una de las más comunes. Calcular el área de un triángulo es fundamental en muchas situaciones, ya sea en matemáticas, física o construcción. Afortunadamente, eisten fórmulas sencillas que nos permiten determinar el área de un triángulo con precisión.

Fórmula del área de un triángulo equilátero

Un triángulo equilátero es aquel que tiene todos sus lados iguales. Para calcular su área, utilizamos la siguiente fórmula:

Área = (lado * lado * √3) / 4

Donde "lado" es la longitud de uno de los lados del triángulo.

Fórmula del área de un triángulo isósceles

Un triángulo isósceles es aquel que tiene dos lados iguales y uno distinto. Para calcular su área, utilizamos la siguiente fórmula:

Área = (base * altura) / 2

Donde "base" es la longitud del lado desigual y "altura" es la distancia desde el lado desigual hasta la base del triángulo.

Fórmula del área de un triángulo escaleno

Un triángulo escaleno es aquel que tiene todos sus lados y ángulos diferentes entre sí. Para calcular su área, utilizamos la siguiente fórmula conocida como la Fórmula de Herón:

Área = √(s * (s - a) * (s - b) * (s - c))

Donde "a", "b" y "c" son las longitudes de los lados del triángulo, y "s" es el semiperímetro, que se calcula sumando los tres lados y dividiéndolo entre 2.

Ejemplo práctico: calcular el área de un triángulo equilátero

Supongamos que tenemos un triángulo equilátero con un lado de longitud 5 cm. Utilizando la fórmula mencionada anteriormente, procedemos a calcular su área:

Área = (5 * 5 * √3) / 4 = (25 * √3) / 4 ≈ 10.82 cm²

Por lo tanto, el área de este triángulo equilátero sería aproimadamente 10.82 cm².

Cómo se puede calcular rápidamente el área de un cuadrado o rectángulo

Calcular el área de un cuadrado o rectángulo es una tarea bastante sencilla y rápida. Para ello, solo necesitamos conocer la medida de uno de sus lados y seguir una fórmula muy simple.

La fórmula para calcular el área de un cuadrado o rectángulo es simplemente multiplicar la longitud de su base por la longitud de su altura. Es decir:

Área = Base * Altura

Por ejemplo, si tenemos un cuadrado con una base de 5 metros y una altura de 5 metros, podemos calcular su área de la siguiente manera:

Área = 5 m * 5 m = 25 m²

De esta forma obtenemos que el área del cuadrado es de 25 metros cuadrados.

Si en cambio tenemos un rectángulo con una base de 8 metros y una altura de 6 metros, podemos aplicar la misma fórmula:

Área = 8 m * 6 m = 48 m²

En este caso, el área del rectángulo sería de 48 metros cuadrados.

Como puedes ver, calcular el área de un cuadrado o rectángulo es realmente simple. Solo necesitas conocer las medidas de la base y la altura y aplicar la fórmula adecuada. ¡Inténtalo tú mismo y verás lo fácil que es!

Cuál es la fórmula para encontrar el área de un círculo y cómo se utiliza

El área de un círculo es una magnitud geométrica que determina la cantidad de superficie que ocupa dicho círculo en un plano. Calcular el área de un círculo es sumamente importante en diversos campos como la geometría, la física, la ingeniería y muchas otras disciplinas.

En matemáticas, la fórmula más comúnmente utilizada para encontrar el área de un círculo es: A = π * r^2, donde A representa el área, π es una constante aproimadamente igual a 3.14159 y r es el radio del círculo.

Para aplicar esta fórmula, es necesario conocer el valor del radio del círculo. El radio es la distancia que eiste desde el centro del círculo hasta cualquier punto sobre su borde. Una vez que se conoce el radio, simplemente se debe sustituir dicho valor en la fórmula y realizar el cálculo correspondiente.

Veamos un ejemplo práctico. Supongamos que tenemos un círculo con un radio de 5 unidades. Para calcular el área de este círculo, debemos utilizar la fórmula mencionada previamente. Sustituimos el valor del radio:

A = π * (5)^2

Ahora procedemos a realizar las operaciones matemáticas:

A = 3.14159 * 25

Finalmente, obtenemos el resultado:

A ≈ 78.54 unidades cuadradas

La unidad de medida utilizada en el resultado dependerá de las unidades utilizadas para el radio. En este caso, utilizamos unidades cuadradas debido a que se trata de un área.

Es importante destacar que la fórmula para calcular el área de un círculo es solo aplicable a los círculos perfectos, es decir, aquellos que tienen una forma perfectamente redonda y simétrica. En casos de circunferencias irregulares o elipses, se deben utilizar fórmulas diferentes específicamente diseñadas para cada tipo de figura geométrica.

Calcular el área de un círculo es una operación sencilla pero fundamental en diversas áreas del conocimiento. La fórmula A = π * r^2 permite obtener un resultado preciso para determinar cuánto espacio ocupa un círculo en un plano. Recuerda tener en cuenta las unidades de medida utilizadas tanto en el radio como en el área resultante para interpretar correctamente el valor obtenido.

Qué método puedo usar para calcular el área de un trapezoide

El cálculo del área de un trapezoide es un proceso relativamente sencillo que se basa en la fórmula específica para esta figura geométrica. Un trapezoide es un polígono de cuatro lados, donde dos de ellos son paralelos y los otros dos no lo son. Para calcular su área, necesitamos conocer la longitud de las bases y la altura.

La fórmula general para calcular el área de un trapezoide es:

Área = (Base mayor + Base menor) * Altura / 2

Para entender mejor cómo funciona esta fórmula, vamos a desglosarla paso a paso. Primero, identificamos cuál es la base mayor y cuál es la base menor del trapezoide. La base mayor es el lado paralelo más largo, mientras que la base menor es el lado paralelo más corto.

A continuación, necesitamos conocer la altura del trapezoide, que es la distancia perpendicular entre las bases. Esta medida nos indica qué tan alto es el trapezoide en relación con sus bases y es fundamental para calcular el área correctamente.

Una vez que tenemos identificadas las bases y la altura, podemos aplicar la fórmula mencionada anteriormente. Sumamos las longitudes de las bases mayor y menor y multiplicamos por la altura. Finalmente, dividimos este resultado entre 2 para obtener el área total del trapezoide.

Veamos un ejemplo práctico para ilustrar mejor el proceso de cálculo del área de un trapezoide. Supongamos que tenemos un trapezoide con una base mayor de 10 cm, una base menor de 6 cm y una altura de 8 cm.

Área = (10 cm + 6 cm) * 8 cm / 2

Primero sumamos las bases:

Área = 16 cm * 8 cm / 2

Luego multiplicamos por la altura:

Área = 128 cm² / 2

Finalmente, dividimos el resultado entre 2:

Área = 64 cm²

Por lo tanto, el área de este trapezoide en particular sería de 64 centímetros cuadrados.

Es importante recordar que, al realizar cálculos de áreas, es necesario utilizar unidades de medida coherentes. En el ejemplo anterior, todas las dimensiones del trapezoide se epresaron en centímetros (cm), por lo que el área resultante también está en centímetros cuadrados (cm²).

Ahora que conoces cómo calcular el área de un trapezoide, puedes aplicar esta fórmula a otros ejemplos y figuras geométricas similares. Recuerda siempre identificar correctamente las bases y la altura para obtener resultados precisos. ¡Practica y disfruta eplorando el fascinante mundo de las formas y sus áreas!

Cuáles son las fórmulas para hallar el área de un pentágono regular e irregular

El cálculo del área de una figura geométrica es una tarea común en matemáticas y física. En este artículo, te eplicaremos cómo calcular el área de un pentágono, tanto regular como irregular. Ambas formas requieren diferentes fórmulas y enfoques para obtener resultados precisos.

Cálculo del área de un pentágono regular

Un pentágono regular es aquel que tiene todos sus lados y ángulos iguales. Esto hace que el cálculo de su área sea más sencillo, ya que puedes utilizar una fórmula específica para encontrarla.

Para hallar el área de un pentágono regular, necesitarás conocer la medida de uno de sus lados y el apotema, que es una línea perpendicular a uno de los lados y que llega al centro del pentágono.

La fórmula para calcular el área de un pentágono regular es:

Área = (perímetro * apotema) / 2

Donde el perímetro se obtiene multiplicando la medida de uno de los lados por 5, ya que un pentágono regular tiene cinco lados iguales.

Una vez que hayas calculado el área, asegúrate de indicar las unidades de medida utilizadas, como metros cuadrados o centímetros cuadrados, dependiendo del sistema utilizado.

Cálculo del área de un pentágono irregular

En el caso de un pentágono irregular, donde sus lados y ángulos no son iguales, el cálculo del área es un poco más complejo. Aquí, necesitarás dividir el pentágono en triángulos más pequeños y utilizar fórmulas para calcular las áreas de cada uno de ellos.

Puedes utilizar diferentes métodos para dividir el pentágono en triángulos, como trazar diagonales o usar la fórmula del área de un triángulo conocida como "semi perímetro".

Una vez que has dividido el pentágono en triángulos individuales, podrás calcular el área de cada uno de ellos utilizando la siguiente fórmula:

Área de un triángulo = (base * altura) / 2

Suma todas las áreas de los triángulos para obtener el área total del pentágono irregular.

Recuerda siempre indicar las unidades de medida utilizadas para evitar confusiones.

El cálculo del área de un pentágono puede ser sencillo o complejo dependiendo de si es regular o irregular. Si conoces las medidas adecuadas de los lados y apotema en el caso de un pentágono regular, puedes utilizar una fórmula específica. Sin embargo, en el caso de un pentágono irregular, necesitarás descomponer la figura en triángulos más pequeños y calcular el área de cada uno de ellos.

Esperamos que este artículo te haya sido útil para comprender cómo calcular el área de un pentágono de forma sencilla y precisa. Recuerda practicar con diferentes ejemplos para afianzar tus conocimientos en geometría.

Cómo se calcula el área de un heágono sin complicaciones

El cálculo del área de un heágono puede parecer complicado a primera vista, pero en realidad es bastante sencillo si se siguen los pasos adecuados. En este artículo, te mostraremos cómo calcular el área de un heágono de forma precisa y sin complicaciones.

Paso 1: Identificar el tipo de heágono

Lo primero que debemos hacer es identificar el tipo de heágono del cual queremos calcular el área. Un heágono regular tiene todos sus lados y ángulos iguales, mientras que un heágono irregular tiene lados y ángulos de diferentes medidas. Dependiendo del tipo de heágono, utilizaremos diferentes fórmulas para realizar el cálculo del área.

Paso 2: Medir los lados del heágono

A continuación, debemos medir los lados del heágono. Si se trata de un heágono regular, bastará con medir uno de sus lados, ya que todos tendrán la misma medida. En cambio, si estamos trabajando con un heágono irregular, deberemos medir los seis lados por separado.

Paso 3: Calcular el área del heágono regular

Si el heágono es regular, podemos utilizar la siguiente fórmula para calcular su área:

Área = ((lado^2) * (√3)) / 4

Donde "lado" representa la medida de un lado del heágono. Para obtener el área, simplemente elevamos al cuadrado la medida de uno de los lados, lo multiplicamos por la raíz cuadrada de 3 y finalmente dividimos el resultado entre 4.

Paso 4: Calcular el área del heágono irregular

Si el heágono es irregular, el cálculo del área puede ser un poco más complejo. En este caso, podemos dividir el heágono en triángulos más pequeños y calcular el área de cada uno de ellos por separado. Luego, sumamos las áreas de los triángulos para obtener el área total del heágono irregular.

Paso 5: Ejemplo práctico

Para entender mejor cómo se realiza el cálculo del área de un heágono, veamos un ejemplo práctico:

Supongamos que tenemos un heágono regular con un lado de longitud 5 cm. Utilizando la fórmula mencionada en el paso 3, podemos calcular su área de la siguiente manera:

Área = ((5^2) * (√3)) / 4
= (25 * √3) / 4
≈ 10.825 cm^2

De esta manera, hemos calculado el área del heágono regular correctamente.

Recuerda que, cuando estés calculando el área de un heágono irregular, deberás descomponerlo en triángulos y calcular el área de cada uno por separado antes de sumarlos.

Ahora que conoces estos sencillos pasos, puedes calcular el área de un heágono sin complicaciones. ¡Pon a prueba tus conocimientos y descubre la superficie de cualquier heágono que encuentres!

Cuál es la ecuación que nos permite encontrar el área de un paralelogramo

El cálculo del área de un paralelogramo es bastante sencillo y se puede realizar utilizando una fórmula específica. Para encontrar el área de esta figura geométrica, debemos conocer la longitud de su base y la altura correspondiente.

La fórmula para calcular el área de un paralelogramo es:

Área = base altura

Donde la base representa el lado del paralelogramo sobre el cual se encuentra la altura. La altura, por otro lado, es la distancia perpendicular entre la base y el lado contrario.

Para aplicar esta fórmula, es importante que la base y la altura estén epresadas en las mismas unidades de medida. Si no es así, es necesario convertir las medidas a la misma unidad antes de realizar el cálculo.

Ejemplo práctico: cálculo del área de un paralelogramo

Supongamos que tenemos un paralelogramo con una base de 8 centímetros y una altura de 5 centímetros. Aplicando la fórmula mencionada anteriormente, podemos encontrar su área de la siguiente manera:

Área = 8 cm 5 cm

Realizando la multiplicación, obtendremos:

Área = 40 cm²

Por lo tanto, el área de este paralelogramo en particular es de 40 centímetros cuadrados.

Es importante resaltar que esta fórmula solo es aplicable a paralelogramos. Si estamos calculando el área de otra figura geométrica, como un triángulo o un círculo, se deberán utilizar fórmulas distintas.

Para calcular el área de un paralelogramo, es necesario multiplicar la longitud de su base por la altura correspondiente. Conociendo esta fórmula y aplicándola correctamente, podremos obtener el área de cualquier paralelogramo sin dificultad.

Eiste alguna fórmula especial para calcular el área de un rombo

Sí, eisten fórmulas específicas para calcular el área de diferentes figuras geométricas y en el caso del rombo no es una ecepción. El rombo es un polígono de cuatro lados con lados iguales y diagonales perpendiculares entre sí. Calcular su área puede ser muy sencillo si conocemos la longitud de las diagonales.

La fórmula para calcular el área de un rombo es bastante simple y directa. Solo necesitamos tener información confiable sobre la longitud de las diagonales, ya que este dato será clave para resolver el problema. A continuación, te mostraré cómo aplicar esta fórmula paso a paso.

Paso 1: Obtener la longitud de las diagonales

<p>Para calcular el área de un rombo, necesitaremos conocer la longitud de sus diagonales. La diagonal principal (d₁) y la diagonal secundaria (d₂).</p>

• Por ejemplo, supongamos que la longitud de la diagonal principal (d₁) es de 10 centímetros.
• Y también supongamos que la longitud de la diagonal secundaria (d₂) es de 8 centímetros.

Ahora que tenemos los valores de las diagonales, estamos listos para calcular el área del rombo.

Paso 2: Aplicar la fórmula del área del rombo

<p>Para calcular el área de un rombo, simplemente multiplicamos el producto de las diagonales y lo dividimos entre 2. Siguiendo la fórmula: A = (d₁ * d₂) / 2.</p>

Utilizando los valores de las diagonales que mencionamos anteriormente, podemos calcular el área de la siguiente manera:

<p>A = (10 cm * 8 cm) / 2</p>

Paso 3: Realizar la operación matemática

<p>Para obtener el resultado final, simplemente realizamos la operación matemática indicada por la fórmula.</p>

Continuando con el ejemplo, realizamos la operación:

<p>A = 80 cm² / 2</p>

Ahora solo nos queda simplificar la epresión:

<p>A = 40 cm²</p>

Finalmente, hemos obtenido el área del rombo, que en este caso es de 40 centímetros cuadrados.

Recuerda siempre identificar correctamente las diagonales y asegurarte de que sus valores sean consistentes y precisos para obtener un cálculo del área correcto. ¡Ahora ya sabes cómo calcular el área de un rombo de forma sencilla y precisa!

Qué pasos debo seguir para calcular el área de un polígono irregular

Calcular el área de un polígono irregular puede parecer complicado, pero en realidad es más sencillo de lo que parece. Solo necesitas seguir algunos pasos y tener en cuenta algunas fórmulas básicas de geometría.

A continuación, te mostraré los pasos que debes seguir para calcular el área de un polígono irregular:

Paso 1: Divide el polígono

Lo primero que debes hacer es dividir el polígono irregular en triángulos o cuadriláteros más simples. Esto se debe a que el área de un triángulo o cuadrilátero es más fácil de calcular que la de un polígono irregular.

Puedes elegir diferentes puntos dentro del polígono para trazar las diagonales o divisiones. La idea es obtener triángulos o cuadriláteros que sean lo más regulares posible.

Paso 2: Calcula el área de cada figura

Una vez que hayas dividido el polígono en figuras más simples, debes calcular el área de cada una de ellas. Para un triángulo, puedes utilizar la fórmula del área de un triángulo:

Área = (base altura) / 2

Recuerda que la base y la altura deben ser perpendiculares entre sí.

Para un cuadrilátero, puedes utilizar la fórmula del área de un cuadrilátero:

Área = (diagonal mayor diagonal menor) / 2

Si el cuadrilátero es un rectángulo, también puedes utilizar la fórmula del área de un rectángulo:

Área = base altura

Paso 3: Suma las áreas

Una vez que hayas calculado el área de cada figura, debes sumar todas las áreas para obtener el área total del polígono irregular. Simplemente suma todas las áreas obtenidas en el paso anterior.

Paso 4: Redondea el resultado

Finalmente, debes redondear el resultado a un número apropiado de decimales según sea necesario. El número de decimales dependerá de la precisión requerida para tu cálculo o aplicación específica.

Recuerda que algunos polígonos irregulares pueden tener partes cóncavas. En este caso, debes dividir el polígono en partes más pequeñas y aplicar los pasos anteriores a cada una de ellas para obtener el área total del polígono.

Calcular el área de un polígono irregular implica dividirlo en figuras más simples, calcular el área de cada una de estas figuras, sumar las áreas y redondear el resultado. Siguiendo estos pasos, podrás calcular el área de cualquier polígono irregular de forma sencilla y precisa.

Cuál es la manera más sencilla de calcular el área de una figura tridimensional, como un cubo o una esfera

Calcular el área de una figura geométrica tridimensional puede parecer intimidante al principio, pero en realidad hay formas sencillas y precisas de hacerlo. En este artículo te eplicaremos cómo calcular el área de dos figuras tridimensionales populares: el cubo y la esfera.

Cómo calcular el área de un cubo

Un cubo es una figura tridimensional que tiene seis caras cuadradas idénticas. Para calcular el área total de un cubo, simplemente tienes que sumar el área de cada una de sus caras.

El área de una cara de un cubo se calcula multiplicando la longitud de uno de los lados del cuadro por sí mismo. Así que si la longitud de un lado del cuadro es "a", el área de una cara sería a a = a^2.

Dado que hay seis caras iguales en un cubo, simplemente tienes que multiplicar el área de una cara por 6 para obtener el área total del cubo. Por lo tanto, el área total del cubo se calcula así: Área total = 6 a^2.

Por ejemplo, si tienes un cubo con un lado de longitud 5 cm, puedes calcular el área total así: Área total = 6 5^2 = 6 25 = 150 cm^2. Así que el área total de ese cubo sería de 150 centímetros cuadrados.

Cómo calcular el área de una esfera

Una esfera es una figura tridimensional completamente redonda sin caras planas. Calcular el área de una esfera requiere el uso de la fórmula del área de una esfera.

La fórmula del área de una esfera es A = 4πr^2, donde A representa el área de la esfera y r representa el radio de la esfera.

Para calcular el área de una esfera, primero debes conocer el valor del radio. El radio es la distancia desde el centro de la esfera hasta cualquier punto en su superficie. Una vez que tienes el valor del radio, simplemente lo elevas al cuadrado, lo multiplicas por 4 y luego lo multiplicar por π (pi).

Por ejemplo, si tienes una esfera con un radio de 3 cm, puedes calcular el área así: Área = 4 π 3^2 = 4 π 9 = 36π cm^2. Así que el área total de esa esfera sería de 36π centímetros cuadrados.

Recuerda que π (pi) es una constante que se aproima a 3,14159, por lo que el resultado final puede ser aproimado o redondeado dependiendo de la precisión requerida en el cálculo.

El cálculo del área de una figura tridimensional como un cubo o una esfera puede ser realizado utilizando fórmulas simples y precisas. Siempre asegúrate de conocer las dimensiones necesarias, como los lados del cubo o el radio de la esfera, y sigue los pasos adecuados para obtener el área total de la figura deseada.

El área de un cuadrado se calcula multiplicando el valor de uno de sus lados por sí mismo.

La fórmula para calcular el área de un triángulo es: base altura dividido por 2.

El área de un círculo se calcula multiplicando el valor de pi por el radio al cuadrado.

La fórmula del área de un rectángulo es: base altura.

El área de un trapecio se obtiene multiplicando la suma de sus bases por la altura y dividiendo el resultado entre 2.