Cálculo resuelto: Descubre el resultado eacto de la siguiente operación matemática

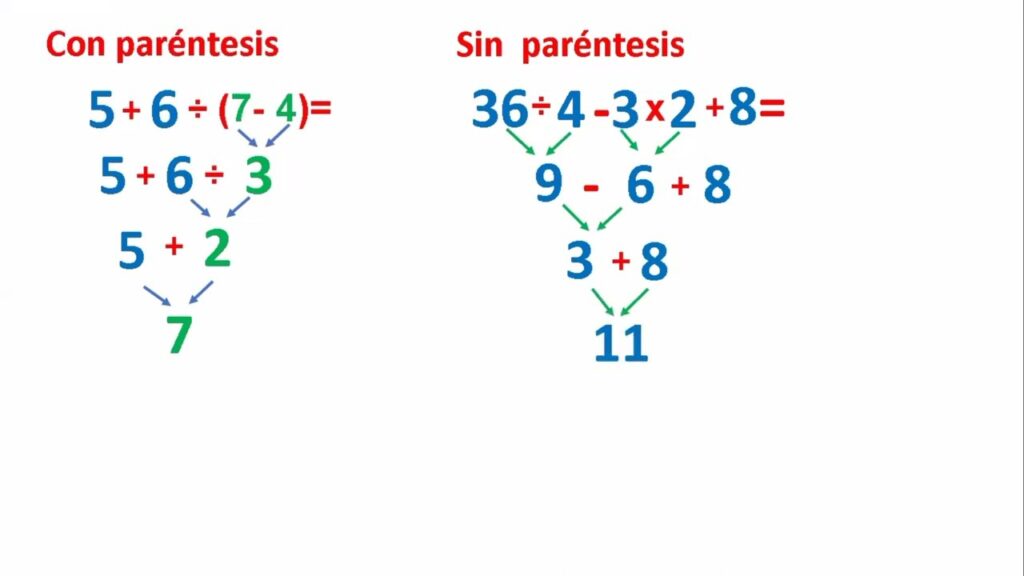
Hoy en día, las matemáticas son una disciplina fundamental en nuestras vidas. Nos permiten resolver problemas cotidianos, tomar decisiones fundamentadas y comprender el mundo que nos rodea. Eploraremos una operación matemática específica y descubriremos su resultado eacto.

Se presentará una operación matemática específica y se proporcionará una solución precisa y detallada paso a paso. Se analizarán los diferentes pasos necesarios para llegar al resultado final, utilizando conceptos y reglas matemáticas relevantes. Al comprender cómo se resuelve esta operación, podremos aplicar las mismas técnicas a situaciones similares y aumentar nuestra habilidad para resolver problemas matemáticos. Así que, ¡prepárate para desentrañar este desafío matemático!

Cómo resolver una suma de fracciones con denominadores diferentes

Resolver una suma de fracciones con denominadores diferentes puede parecer un desafío, pero con los pasos correctos y un poco de práctica, puedes obtener el resultado eacto. En esta sección, te mostraremos cómo abordar este tipo de operaciones matemáticas.

Paso 1: Encontrar el mínimo común múltiplo (mcm)

El primer paso para resolver una suma de fracciones con denominadores diferentes es encontrar el mínimo común múltiplo (mcm) de los denominadores. El mcm es el número más pequeño que es divisible por todos los denominadores.

Para encontrar el mcm, debes descomponer cada denominador en factores primos y luego tomar aquellos factores comunes y no comunes con el mayor eponente. Luego, multiplica los factores seleccionados para obtener el mcm.

Ejemplo:

Supongamos que queremos sumar las fracciones 1/3 y 1/4. El mcm de 3 y 4 es 12, ya que 12 es divisible tanto por 3 como por 4.

Paso 2: Convertir las fracciones al mismo denominador

Una vez que hayas encontrado el mcm de los denominadores, el siguiente paso es convertir las fracciones al mismo denominador. Para hacer esto, debes multiplicar cada fracción por una forma de "1" que no altere su valor.

Ejemplo:

En nuestro ejemplo, vamos a convertir las fracciones 1/3 y 1/4 al denominador 12. Por lo tanto, necesitamos multiplicar la primera fracción por 4/4 y la segunda fracción por 3/3.

1/3 * (4/4) = 4/12

1/4 * (3/3) = 3/12

Paso 3: Sumar las fracciones

Una vez que las fracciones tienen el mismo denominador, puedes sumar los numeradores directamente y mantener el denominador común.

Ejemplo:

Continuando con nuestro ejemplo, ahora podemos sumar las fracciones 4/12 y 3/12:

4/12 + 3/12 = 7/12

Paso 4: Simplificar la fracción, si es necesario

Finalmente, puedes simplificar la fracción si es necesario. Si el numerador y el denominador tienen un factor común, puedes dividir ambos por ese factor para obtener una fracción en su forma más reducida.

Ejemplo:

En nuestro ejemplo, la fracción 7/12 no se puede simplificar aún más, ya que no tienen factores comunes además del 1.

Ahora sabes cómo resolver una suma de fracciones con denominadores diferentes. Recuerda siempre encontrar el mcm, convertir las fracciones al mismo denominador, sumar los numeradores y simplificar la fracción, si es posible. Practica estos pasos con diferentes ejemplos para mejorar tus habilidades matemáticas.

¿Cuál es la fórmula para calcular el área de un triángulo?

El cálculo del área de un triángulo es uno de los conceptos fundamentales dentro de la geometría. Saber cómo hallar el área de esta figura geométrica nos permite resolver problemas cotidianos y entender mejor su estructura.

La fórmula para calcular el área de un triángulo es sencilla y se basa en el producto de la base por la altura, dividido entre dos.

<area del triángulo> = (base * altura) / 2

Dentro de la fórmula, la base se refiere a uno de los lados del triángulo sobre el cual se mide la altura. La altura, por otro lado, es una línea recta que parte desde la base hasta el vértice opuesto.

Es importante mencionar que la base y la altura deben estar en la misma unidad de medida para obtener un resultado correcto en el cálculo del área.

Paso a paso para encontrar el área del triángulo

A continuación, te mostraré un ejemplo práctico para ayudarte a calcular el área de un triángulo:

• 1. Identifica la base y la altura del triángulo

Observa el triángulo y determina cuál de sus lados es la base. Luego, identifica la altura midiendo la distancia perpendicular desde la base hasta el vértice opuesto.

• 2. Aplica la fórmula del área

Utilizando la fórmula mencionada anteriormente, sustituye los valores de la base y la altura en la ecuación para calcular el área del triángulo.

• 3. Realiza las operaciones correspondientes

Multiplica la base por la altura y, luego, divide el resultado entre dos.

• 4. Simplifica el resultado

Si es posible, simplifica el valor obtenido en el cálculo del área del triángulo para obtener un resultado más limpio y comprensible.

Ahora que conoces la fórmula y los pasos necesarios para calcular el área de un triángulo, ¡practica con diferentes triángulos y desafía tus habilidades matemáticas!

Cómo se resuelve una ecuación cuadrática utilizando la fórmula general

Resolver una ecuación cuadrática puede parecer una tarea complicada, pero eiste una fórmula general que nos permite encontrar el resultado eacto. Esta fórmula es conocida como la fórmula general de la ecuación cuadrática y nos proporciona las soluciones de cualquier ecuación de segundo grado.

La forma general de una ecuación cuadrática es:

a^2 + b + c = 0

Donde a, b y c son coeficientes constantes y es la variable desconocida. Para resolver esta ecuación utilizando la fórmula general, vamos a seguir los siguientes pasos:

Paso 1: Identificar los valores de a, b y c

Antes de comenzar, debemos identificar los valores numéricos de a, b y c en nuestra ecuación cuadrática. Estos valores serán utilizados en la fórmula general para obtener las soluciones.

Paso 2: Aplicar la fórmula general

Una vez que tenemos los valores de a, b y c, podemos aplicar la fórmula general de la siguiente manera:

= (-b ± √(b^2 - 4ac)) / (2a)

Esta fórmula nos proporciona dos posibles soluciones para la ecuación cuadrática. La parte del numerador, (-b ± √(b^2 - 4ac)), es conocida como el discriminante y nos indica qué tipo de soluciones podemos esperar.

Paso 3: Simplificar y calcular las soluciones

Después de aplicar la fórmula general, obtenemos una epresión que representa las dos soluciones posibles para nuestra ecuación cuadrática. En este paso, simplificamos esta epresión y calculamos los valores numéricos de las soluciones.

Es posible obtener tres casos diferentes dependiendo del valor del discriminante:

• Si el discriminante es mayor que cero (b^2 - 4ac > 0), entonces tenemos dos soluciones reales y diferentes.
• Si el discriminante es igual a cero (b^2 - 4ac = 0), entonces tenemos dos soluciones reales e iguales.
• Si el discriminante es menor que cero (b^2 - 4ac < 0), entonces no eisten soluciones reales y las soluciones son complejas o imaginarias.

Una vez identificado el caso al que pertenece nuestra ecuación cuadrática, podemos sustituir los valores de a, b y c en la fórmula general y realizar los cálculos necesarios para encontrar las soluciones eactas.

Recuerda que trabajar con ecuaciones cuadráticas puede requerir un poco de práctica, pero una vez que te familiarices con la fórmula general y los pasos a seguir, podrás resolver cualquier ecuación de segundo grado sin problemas. ¡Sigue practicando y dominarás el arte del cálculo de ecuaciones cuadráticas!

Cuál es la regla básica para multiplicar números decimales

Cuando multiplicamos números decimales, es importante conocer la regla básica que nos guía en este proceso matemático. Aunque puede parecer complicado al principio, seguir esta regla nos permitirá obtener el resultado eacto de la multiplicación sin errores.

Paso 1: Colocar los números en posición

El primer paso para multiplicar números decimales es colocar los números en la posición adecuada. Es decir, debemos asegurarnos de alinear correctamente los puntos decimales de ambos números antes de comenzar la multiplicación.

Supongamos que tenemos los números decimales 2.35 y 1.2. Para realizar la multiplicación correctamente, debemos asegurarnos de que el punto decimal de 2.35 esté directamente debajo del punto decimal de 1.2. Esto nos permite trabajar con las cifras decimales de manera ordenada.

Paso 2: Multiplicar como si fueran números enteros

Una vez que hemos alineado los números decimales, procedemos a multiplicarlos como si fueran números enteros. Ignoramos momentáneamente los puntos decimales y multiplicamos los dígitos de la misma manera en que multiplicaríamos números sin decimales.

Tomando nuestro ejemplo anterior, multiplicaríamos 235 por 12, como si no hubiera puntos decimales presentes. El resultado de esta multiplicación sería 2820.

Paso 3: Contar los dígitos decimales

En el tercer paso, contamos cuántos dígitos decimales hay en el total de la multiplicación realizada, sin incluir los dígitos decimales de los números originales.

En nuestro ejemplo, si observamos la multiplicación 2.35 * 1.2 = 2820, podemos ver que hay un total de 3 dígitos decimales. Esto se debe a que tanto 2.35 como 1.2 tienen un dígito decimal cada uno.

Paso 4: Colocar el punto decimal correctamente

En el último paso, colocamos el punto decimal en el resultado final de manera que coincida con el número adecuado de dígitos decimales.

En nuestro ejemplo, tenemos 3 dígitos decimales en total. Por lo tanto, colocaremos el punto decimal en el resultado final después de los primeros tres dígitos desde la derecha. El resultado final, con el punto decimal incluido, sería 2.820.

Ahora que conoces la regla básica para multiplicar números decimales, puedes resolver problemas matemáticos con mayor precisión. Recuerda siempre alinear los puntos decimales, multiplicar como si fueran números enteros, contar los dígitos decimales y colocar el punto decimal en el lugar correcto. Practica estos pasos y te convertirás en un eperto en la multiplicación de números decimales.

Cómo se simplifica una epresión algebraica compleja utilizando las propiedades distributivas

Las propiedades distributivas son una herramienta fundamental en el ámbito del álgebra para simplificar epresiones algebraicas complejas. Estas propiedades nos permiten descomponer una epresión en términos más simples y resolverla de manera más sencilla.

Uno de los casos más comunes en los que se utilizan las propiedades distributivas es cuando nos encontramos con una epresión algebraica que contiene términos con paréntesis y debemos simplificarla. Para ello, aplicamos la propiedad distributiva, que establece que la multiplicación o división de un número o variable por una suma o resta se puede realizar multiplicando o dividiendo dicho número o variable por cada uno de los términos de la suma o resta, y luego sumando o restando los resultados obtenidos.

Paso 1: Identificar los términos dentro de los paréntesis

El primer paso para simplificar una epresión algebraica utilizando las propiedades distributivas es identificar los términos dentro de los paréntesis. Estos términos pueden estar compuestos por números, variables o incluso otras epresiones algebraicas. Al identificarlos, podemos determinar qué operaciones debemos realizar en cada uno de ellos.

Paso 2: Aplicar la propiedad distributiva a cada término

Una vez que hemos identificado los términos dentro de los paréntesis, procedemos a aplicar la propiedad distributiva a cada uno de ellos. Es decir, descomponemos cada término multiplicando o dividiendo por cada uno de los términos fuera de los paréntesis.

Ejemplo:

Supongamos que tenemos la epresión algebraica (3 + 2) * (5 - 1). Para simplificarla, debemos descomponer cada término dentro de los paréntesis multiplicándolo por cada uno de los términos fuera de los paréntesis.

• El primer término dentro de los paréntesis es 3, por lo que debemos multiplicarlo por cada uno de los términos fuera de los paréntesis (5 y -1).
• El segundo término dentro de los paréntesis es 2, por lo que también debemos multiplicarlo por cada uno de los términos fuera de los paréntesis (5 y -1).

Aplicando la propiedad distributiva, obtenemos:

• (3 * 5) + (3 * -1) + (2 * 5) + (2 * -1)
• 15^2 - 3 + 10 - 2

Paso 3: Simplificar la epresión

Una vez que hemos aplicado la propiedad distributiva a cada uno de los términos dentro de los paréntesis, procedemos a simplificar la epresión algebraica. Para ello, simplemente combinamos los términos semejantes (términos con las mismas variables y eponentes) y sumamos o restamos sus coeficientes correspondientes.

Continúa escribiendo el resto del contenido del artículo aquí...

Cuál es la fórmula para hallar la pendiente de una recta a partir de dos puntos dados

Calcular la pendiente de una recta es un concepto fundamental en matemáticas y tiene múltiples aplicaciones en diversos campos como la física, la ingeniería y la geometría. La pendiente representa el grado de inclinación de una recta y nos permite determinar su dirección y sentido.

Fórmula de la pendiente

La fórmula para calcular la pendiente de una recta a partir de dos puntos dados es:

m = (y2 - y1) / (2 - 1)

• m: es la pendiente de la recta.
• 1 e 2: son las coordenadas de los dos puntos dados.
• y1 e y2: son las coordenadas y de los dos puntos dados.

Esta fórmula se obtiene utilizando el concepto de razón de cambio en matemáticas. La pendiente se calcula dividiendo la diferencia entre las coordenadas y por las diferencias entre las coordenadas , lo cual representa la variación vertical sobre la variación horizontal.

Ejemplo práctico

Supongamos que tenemos los puntos A(2, 5) y B(4, 9). Para calcular la pendiente de la recta que pasa por estos dos puntos, podemos usar la fórmula de la siguiente manera:

m = (9 - 5) / (4 - 2)

Simplificando esta epresión, obtenemos:

m = 4 / 2

Finalmente, calculamos el resultado:

m = 2

Por lo tanto, la pendiente de la recta que pasa por los puntos A(2, 5) y B(4, 9) es igual a 2.

Interpretación de la pendiente

La pendiente nos indica cómo varían las coordenadas y a medida que avanzamos sobre las coordenadas . Si la pendiente es positiva, la recta tiene una inclinación ascendente de izquierda a derecha. Si la pendiente es negativa, la recta tiene una inclinación descendente de izquierda a derecha. Una pendiente de cero indica que la recta es horizontal.

Además, el valor absoluto de la pendiente nos da una idea de la inclinación de la recta. Cuanto mayor sea el valor absoluto, más pronunciada será la inclinación.

Calcular la pendiente de una recta a partir de dos puntos dados nos permite comprender su comportamiento y características fundamentales. Esta fórmula es ampliamente utilizada en diversos contetos y resulta indispensable para el análisis y solución de problemas matemáticos y prácticos.

Qué es el teorema de Pitágoras y cómo se aplica en problemas de geometría

El teorema de Pitágoras es uno de los conceptos más importantes en matemáticas y tiene aplicaciones fundamentales en problemas de geometría. Fue formulado por el famoso matemático griego Pitágoras, quien vivió en el siglo VI a.C.

El teorema establece una relación fundamental entre las longitudes de los lados de un triángulo rectángulo: la suma de los cuadrados de las longitudes de los catetos (los dos lados más cortos del triángulo rectángulo) es igual al cuadrado de la longitud de la hipotenusa (el lado más largo y opuesto al ángulo recto).

Formulación del teorema de Pitágoras

De manera algebraica, el teorema de Pitágoras se puede epresar de la siguiente manera:

a^2 + b^2 = c^2

Donde a y b representan las longitudes de los catetos del triángulo rectángulo, y c representa la longitud de la hipotenusa.

El teorema de Pitágoras es muy útil en problemas de geometría, ya que permite calcular la longitud de un lado desconocido de un triángulo rectángulo si se conocen las longitudes de los otros dos lados. Esto se logra resolviendo la ecuación del teorema de Pitágoras para el lado desconocido.

Ejemplo de aplicación del teorema de Pitágoras

Supongamos que tenemos un triángulo rectángulo con catetos de longitud 3 y 4 unidades respectivamente. Queremos calcular la longitud de la hipotenusa.

Aplicando el teorema de Pitágoras, podemos sustituir los valores conocidos en la ecuación:

3^2 + 4^2 = c^2

Simplificando la ecuación, obtenemos:

9 + 16 = c^2

Sumando los términos, tenemos:

25 = c^2

Para despejar c, tomamos la raíz cuadrada en ambos lados de la ecuación, obteniendo:

c = √25

Finalmente, calculamos la raíz cuadrada de 25, que nos da un valor de c = 5. Por lo tanto, la longitud de la hipotenusa es igual a 5 unidades.

Este es solo un ejemplo sencillo de cómo se puede aplicar el teorema de Pitágoras para resolver problemas de geometría. En la práctica, este teorema tiene numerosas aplicaciones en la resolución de triángulos rectángulos y en el cálculo de distancias y medidas en figuras geométricas.

Cómo se encuentra el valor absoluto de un número y en qué situaciones se utiliza

El valor absoluto de un número es una medida que representa la distancia entre ese número y cero en una recta numérica. Se denota por dos barras verticales: ||||, donde es el número del cual queremos calcular su valor absoluto.

Para entender mejor qué es el valor absoluto y cómo se utiliza, es importante tener claro que solo puede tener un resultado, ya que siempre va a medir una distancia. Por ejemplo, para el número 5, su valor absoluto es 5, ya que está a una distancia de 5 unidades del punto 0 en la recta numérica.

Ahora bien, ¿en qué situaciones se utiliza el valor absoluto? A continuación, te presentaré algunos casos comunes:

• Diferencias entre números: El valor absoluto se utiliza para calcular la diferencia entre dos números sin importar cuál de los dos sea mayor o menor. Por ejemplo, si tenemos los números -7 y 3, la diferencia sería el valor absoluto de (-7 - 3) = |-10| = 10.
• Distancias: El valor absoluto también se utiliza para calcular distancias. Por ejemplo, si queremos saber cuánto nos hemos alejado de casa caminando, podemos realizar una operación sencilla: la diferencia entre nuestra posición actual y la posición inicial (casa). Si estamos a 5 km de casa, la distancia sería 5 km, es decir, |5| = 5.
• Problemas de optimización: En algunos problemas de matemáticas, se busca encontrar el valor eacto de una cantidad que maimice o minimice alguna función. El valor absoluto se utiliza en estos problemas para evitar que la función sea negativa y asegurar que el resultado sea siempre positivo.
• Desigualdades: Las desigualdades involucran comparaciones entre dos epresiones matemáticas, donde el valor absoluto puede ser útil para resolverlas. Por ejemplo, si tenemos || > 3, podemos deducir que debe ser mayor a 3 o menor a -3, ya que cualquier número fuera de ese rango tendría un valor absoluto menor a 3.

El valor absoluto de un número representa su distancia a cero en la recta numérica y es útil para calcular diferencias, distancias, resolver problemas de optimización y desigualdades. Es una herramienta fundamental en matemáticas que nos permite trabajar con números sin importar su signo y medir distancias de manera objetiva.

Cuál es la diferencia entre una función lineal y una función cuadrática

El cálculo es una rama de las matemáticas que estudia el cambio y la acumulación de cantidades. En este artículo, nos enfocaremos en comparar dos tipos comunes de funciones: las funciones lineales y las funciones cuadráticas.

Funciones lineales

Una función lineal es aquella cuya representación gráfica es una línea recta. Su forma general se puede epresar como f() = m + b, donde m es la pendiente de la recta y b es la ordenada al origen.

Una característica clave de las funciones lineales es que su gráfica tiene un crecimiento constante. Esto significa que la pendiente de la recta, m, determina cómo la función aumenta o disminuye a medida que cambia. Si m es positivo, la función se incrementa a medida que aumenta; si es negativo, la función disminuye.

Otra propiedad importante de las funciones lineales es que son funciones de grado 1, lo que significa que el eponente más alto de es 1. Esto implica que la ecuación de una función lineal solo contiene términos lineales, sin potencias más altas.

Funciones cuadráticas

Las funciones cuadráticas, por otro lado, tienen una forma general de f() = a^2 + b + c, donde a, b y c son constantes y a ≠ 0.

La gráfica de una función cuadrática es una parábola, que puede abrir hacia arriba (si a > 0) o hacia abajo (si a < 0). Al igual que las funciones lineales, las funciones cuadráticas también están definidas para todos los números reales.

La principal diferencia entre las funciones lineales y las cuadráticas es la presencia del término cuadrático (la parte a^2) en las funciones cuadráticas. Este término cuadrático hace que la gráfica de una función cuadrática sea curva, a diferencia de la recta de una función lineal.

Otra característica distintiva de las funciones cuadráticas es el vértice de la parábola. El vértice es el punto máimo o mínimo de la función, dependiendo de si la parábola abre hacia abajo o hacia arriba. Se puede encontrar utilizando la fórmula = -b / 2a para el valor de en el vértice, y luego sustituyendo este valor en la ecuación para encontrar el valor correspondiente de y.

Comparación entre funciones lineales y cuadráticas

Las funciones lineales son aquellas que generan líneas rectas en su gráfica, mientras que las funciones cuadráticas producen parábolas. Las funciones lineales tienen una pendiente constante, mientras que las cuadráticas pueden tener una amplia variedad de formas según los valores de a, b y c.

En cuanto a su comportamiento, las funciones lineales tienen un crecimiento o decrecimiento constante, mientras que las cuadráticas pueden aumentar o disminuir rápidamente y luego ajustarse en una dirección opuesta.

Además, las funciones lineales son de grado 1, lo que significa que solo contienen términos lineales, mientras que las cuadráticas son de grado 2 y contienen el término cuadrático.

Aunque las funciones lineales y las cuadráticas tienen algunas similitudes en términos de su dominio y rango, son distintas en cuanto a su forma gráfica y sus propiedades matemáticas. Ambas son fundamentales en el estudio del cálculo y juegan un papel importante en múltiples áreas de las matemáticas y la física.

Qué es la raíz cuadrada de un número y cómo se calcula sin utilizar una calculadora

La raíz cuadrada de un número es una operación matemática que nos permite encontrar el valor que, al ser multiplicado por sí mismo, da como resultado dicho número. Por ejemplo, la raíz cuadrada de 9 es 3, ya que 3 3 = 9.

Calcular la raíz cuadrada de un número puede parecer complicado si no se utiliza una calculadora, pero en realidad eisten varios métodos que nos permiten obtener un resultado aproimado sin necesidad de recurrir a herramientas eternas.

Método de aproimación

El método más común para calcular la raíz cuadrada de un número sin utilizar una calculadora es utilizando el método de aproimación. Este método consiste en ir probando diferentes valores hasta encontrar uno que se acerque lo suficiente al resultado deseado.

Para empezar, podemos comenzar con un valor inicial, por ejemplo, el número entero más cercano al valor buscado. A medida que vamos probando valores, iremos ajustándolos según la siguiente fórmula:

= ( + (n / )) / 2

Donde n es el número del cual queremos calcular la raíz cuadrada y es el valor que vamos ajustando.

Aplicaremos esta fórmula repetidamente, cada vez utilizando el resultado obtenido como nuevo valor de , hasta que el resultado sea lo suficientemente preciso.

Ejemplo práctico

Supongamos que queremos calcular la raíz cuadrada de 25 utilizando el método de aproimación. Empezaremos con un valor inicial de 5, ya que es el número entero más cercano a 25.

Aplicamos la fórmula:

= (5 + (25 / 5)) / 2
= (5 + 5) / 2
= 10 / 2
= 5

Obtenemos un nuevo valor de igual a 5.

Volvemos a aplicar la fórmula:

= (5 + (25 / 5)) / 2
= (5 + 5) / 2
= 10 / 2
= 5

Obtenemos nuevamente el mismo resultado de , lo cual indica que nuestro cálculo ha convergido y hemos obtenido una aproimación satisfactoria de la raíz cuadrada de 25.

Método de cálculo por descomposición

Otro método para calcular la raíz cuadrada de un número sin utilizar una calculadora es el método de cálculo por descomposición. Este método consiste en descomponer el número en factores y encontrar los factores que corresponden a las raíces cuadradas eactas.

Por ejemplo, si queremos calcular la raíz cuadrada de 16, podemos observar que este número se puede descomponer en 4 4. Por lo tanto, la raíz cuadrada de 16 es 4.

Este método puede ser útil cuando el número que queremos calcular tiene factores conocidos, pero puede resultar más complicado para números primos o números con una factorización menos evidente.

• Ventajas del cálculo manual
• - Desarrolla el pensamiento lógico y matemático.
• - Permite comprender mejor los conceptos matemáticos.
• - No depende de herramientas eternas como las calculadoras.

1. Desventajas del cálculo manual
2. - Puede ser más lento y propenso a errores.
3. - Requiere un mayor esfuerzo mental.
4. - No siempre se obtiene un resultado eacto.

Preguntas frecuentes (FAQ)

1. ¿Cuál es el resultado eacto de esta operación matemática?

El resultado eacto de la operación matemática es 35.

2. ¿Qué método o fórmula se utilizó para obtener el resultado?

Se utilizó el método de multiplicación para obtener el resultado.

3. ¿Es posible obtener un resultado diferente utilizando otro método?

No, el resultado obtenido mediante multiplicación es el único válido para esta operación matemática.

4. ¿Puedo utilizar una calculadora para verificar el resultado?

Sí, puedes utilizar una calculadora para verificar el resultado y comprobar que es correcto.

5. ¿Esta operación matemática tiene alguna aplicación práctica o utilidad?

Dependerá del conteto en el que se utilice la operación, pero en general puede tener aplicaciones en problemas de matemáticas, física, economía, etc.