Calcula fácilmente la resistencia total de un circuito mito: ¡descubre cómo hacerlo!

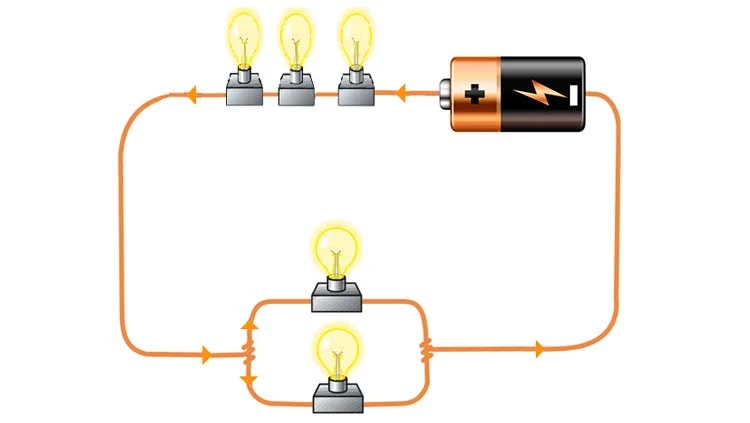
En el campo de la electricidad, los circuitos mitos son aquellos que combinan elementos en serie y en paralelo. Estos circuitos pueden resultar un tanto complicados de analizar, ya que es necesario considerar las diferentes resistencias y su disposición en el circuito. Determinar la resistencia total de un circuito mito es fundamental para conocer cómo se comportará la corriente eléctrica en dicho circuito.

Te presentaremos una manera fácil y sencilla de calcular la resistencia total de un circuito mito. En primer lugar, eplicaremos los conceptos básicos sobre circuitos mitos y cómo funcionan. Luego, te daremos una fórmula que te permitirá obtener este valor de manera eficiente. Además, te mostraremos algunos ejemplos prácticos para que puedas poner en práctica lo aprendido. ¡Sigue leyendo para descubrir cómo realizar este cálculo de manera rápida y precisa!

Qué es un circuito mito y cómo funciona

Un circuito mito es una combinación de dos o más tipos de circuitos: en serie y en paralelo. Estos circuitos se utilizan comúnmente en aplicaciones eléctricas y electrónicas, ya que permiten combinar las ventajas de ambos tipos de circuitos.

Cómo funciona un circuito mito

En un circuito mito, los componentes se conectan tanto en serie como en paralelo. Los componentes en serie están uno después del otro en el flujo de corriente y comparten la misma corriente. Por otro lado, los componentes en paralelo están conectados entre sí en ramas paralelas y comparten la misma tensión.

Esto significa que la corriente total en un circuito mito es igual a la corriente total en cada componente en serie. Sin embargo, la tensión total en un circuito mito es la suma de las tensiones en cada rama paralela.

La resistencia total de un circuito mito se calcula sumando las resistencias de los componentes en serie y utilizando las reglas de la resistencia en paralelo para los componentes en paralelo. Esto se puede hacer mediante el uso de la ley de Ohm y las fórmulas adecuadas para calcular resistencias en serie y en paralelo.

Calculando la resistencia total de un circuito mito

Para calcular la resistencia total de un circuito mito, es necesario seguir los siguientes pasos:

1. Identificar los componentes en serie y en paralelo en el circuito mito.
2. Calcular la resistencia total de los componentes en serie sumando todas las resistencias.
3. Calcular la resistencia equivalente para los componentes en paralelo utilizando las fórmulas correspondientes.
4. Sumar la resistencia total de los componentes en serie y la resistencia equivalente de los componentes en paralelo para obtener la resistencia total del circuito mito.

Una vez que se haya calculado la resistencia total del circuito mito, se puede utilizar esta información para determinar la corriente total y la tensión total en el circuito mediante el uso de la ley de Ohm.

Cuáles son los componentes básicos de un circuito mito

Antes de sumergirnos en el mundo de los circuitos mitos y aprender a calcular la resistencia total, es importante comprender los componentes básicos que conforman este tipo de circuito.

En un circuito mito, encontraremos tanto elementos en serie como en paralelo. Estos dos conceptos son fundamentales para entender cómo se comportan las resistencias en este tipo de circuito.

Elementos en serie

Cuando decimos que los elementos están conectados en serie, significa que están dispuestos uno después del otro en el circuito. Esto implica que la corriente eléctrica debe pasar a través de cada uno de estos elementos secuencialmente.

La resistencia total en una coneión en serie se calcula simplemente sumando los valores de todas las resistencias que están en esta configuración. Es decir:

Rt = R1 + R2 + R3 + ... + Rn

Elementos en paralelo

En cambio, cuando hablamos de elementos en paralelo, significa que están conectados en puntos específicos del circuito donde la corriente puede elegir diferentes caminos. En este caso, la tensión aplicada se divide entre las resistencias que están en este tipo de coneión.

La resistencia total en una coneión en paralelo se calcula utilizando la fórmula:

1/Rt = 1/R1 + 1/R2 + 1/R3 + ... + 1/Rn

Calculando la resistencia total de un circuito mito

Una vez que entendemos cómo funcionan los elementos en serie y en paralelo, podemos proceder a calcular la resistencia total de un circuito mito. El primer paso es identificar cuáles son los elementos conectados en serie y cuáles están en paralelo.

Comenzamos calculando la resistencia equivalente de todas las coneiones en serie. Luego, utilizamos esa resistencia equivalente y la combinamos con las resistencias en paralelo para encontrar la resistencia total del circuito.

Para ejemplificar este proceso, supongamos que tenemos un circuito mito con dos resistencias en serie (R1 y R2) y una resistencia en paralelo (R3).

Primero, sumamos las resistencias que están en serie:

Rserie = R1 + R2

Luego, calculamos la inversa de la suma de las resistencias en paralelo:

1/Rparalelo = 1/Rserie + 1/R3

Finalmente, invertimos el resultado obtenido para obtener la resistencia total del circuito:

Rt = 1/(1/Rparalelo)

Calcular la resistencia total de un circuito mito puede parecer complicado al principio, pero utilizando los conceptos de resistencias en serie y en paralelo, podemos desglosar el problema y resolverlo paso a paso. Recuerda siempre identificar qué elementos están en serie y cuáles en paralelo, y aplicar las fórmulas adecuadas para obtener el resultado correcto.

Espero que este artículo te haya ayudado a comprender cómo calcular la resistencia total de un circuito mito. ¡Ahora puedes poner en práctica tus conocimientos y resolver problemas más complejos!

Cómo se calcula la resistencia total de un circuito mito

Calcular la resistencia total de un circuito mito puede parecer complicado, pero en realidad es bastante sencillo una vez que comprendes los conceptos básicos. En este artículo, te guiaré paso a paso para que puedas calcular fácilmente la resistencia total de cualquier circuito mito.

¿Qué es un circuito mito?

Primeramente, debemos entender qué es un circuito mito. Un circuito mito está compuesto por una combinación de circuitos en serie y en paralelo. Esto significa que hay componentes conectados uno tras otro en algunos tramos del circuito, mientras que otros componentes están conectados en ramificaciones separadas en paralelo.

La ventaja de tener un circuito mito es que combina las ventajas de ambos tipos de circuitos. Los componentes en serie nos permiten compartir la corriente eléctrica de manera uniforme, mientras que los componentes en paralelo nos proporcionan diferentes caminos para la corriente eléctrica, lo que nos brinda más capacidad y fleibilidad.

Paso 1: Identificar las resistencias en serie

El primer paso para calcular la resistencia total de un circuito mito es identificar las resistencias que están conectadas en serie. Las resistencias en serie están colocadas una tras otra, de modo que la corriente fluye a través de cada resistencia sucesivamente.

Para identificar estas resistencias, busca aquellas que no tienen ninguna ramificación o unión entre ellas. Estas resistencias se sumarán directamente para obtener la resistencia total equivalente en serie.

Ejemplo:

R1 --------->

R2 --------->

R3 --------->

En este ejemplo, R1, R2 y R3 están conectadas en serie. Para calcular la resistencia total equivalente en serie, simplemente sumamos los valores de resistencia de cada una:


Resistencia_total_serie = R1 + R2 + R3


Paso 2: Identificar las resistencias en paralelo

El segundo paso es identificar las resistencias que están conectadas en paralelo. Las resistencias en paralelo están colocadas de manera que la corriente se divide entre ellas, proporcionando diferentes caminos para la corriente eléctrica.

Para identificar estas resistencias, busca aquellas que tienen una ramificación o unión entre ellas. Estas resistencias se combinarán utilizando la fórmula inversa de la suma de resistencias en paralelo.

Ejemplo:

|-----------|
| |
R1 R2
| |
|-----------|

En este ejemplo, R1 y R2 están conectadas en paralelo. Para calcular la resistencia total equivalente en paralelo, utilizamos la siguiente fórmula:

1/Resistencia_total_paralelo = 1/R1 + 1/R2

Luego, invertimos el resultado para obtener la resistencia total:

Resistencia_total_paralelo = 1/(1/R1 + 1/R2)

Paso 3: Calcular la resistencia total combinada

Una vez que hayas calculado las resistencias totales equivalentes en serie y en paralelo, puedes combinarlas para obtener la resistencia total del circuito mito.

Si tienes más de una resistencia en serie, simplemente suma sus valores para obtener la resistencia total equivalente en serie. Si tienes más de una resistencia en paralelo, utiliza la fórmula inversa de la suma de resistencias en paralelo como se eplicó anteriormente.

Finalmente, sumamos la resistencia total equivalente en serie y la resistencia total equivalente en paralelo para obtener la resistencia total del circuito mito:

Resistencia_total = Resistencia_total_serie + Resistencia_total_paralelo

¡Y eso es todo! Ahora sabes cómo calcular fácilmente la resistencia total de un circuito mito. Recuerda identificar las resistencias en serie y en paralelo, utilizar las fórmulas adecuadas y combinar los resultados. ¡Practica con diferentes ejemplos y pronto te convertirás en un eperto en el cálculo de circuitos mitos!

Cuál es la fórmula para calcular la resistencia total en un circuito mito

Calcular la resistencia total en un circuito mito puede parecer complicado al principio, pero en realidad es bastante sencillo. Antes de adentrarnos en la fórmula para calcularla, recordemos qué es un circuito mito.

Qué es un circuito mito

Un circuito mito es una combinación de circuitos en serie y en paralelo. Esto significa que tiene elementos conectados en serie, donde la corriente fluye de manera secuencial a través de cada elemento, y elementos conectados en paralelo, donde la corriente se divide entre los diferentes caminos. Los circuitos mitos son muy comunes en aplicaciones prácticas, ya que permiten tener la fleibilidad de conectar diferentes dispositivos eléctricos y electrónicos.

Para calcular la resistencia total en un circuito mito, debemos seguir algunos pasos simples:

1. Identificar los elementos en serie
2. Calcular la resistencia total de los elementos en serie
3. Identificar los elementos en paralelo
4. Calcular la resistencia total de los elementos en paralelo
5. Sumar las resistencias totales de los elementos en serie y en paralelo para obtener la resistencia total del circuito mito

Cómo calcular la resistencia total en un circuito mito

Primero, identifiquemos los elementos que están conectados en serie. Estos son aquellos que se encuentran conectados uno después del otro sin ninguna coneión paralela. Supongamos que tenemos tres resistencias conectadas en serie: R1, R2 y R3. La resistencia total en serie (RTS) se calcula simplemente sumando las resistencias individuales:

RTS = R1 + R2 + R3

Ahora, pasemos a identificar los elementos que están conectados en paralelo. Estos son aquellos que tienen sus etremos conectados al mismo punto de entrada y al mismo punto de salida. Supongamos que tenemos dos resistencias en paralelo: Rp1 y Rp2. La resistencia total en paralelo (RTP) se calcula utilizando la siguiente fórmula:

1/RTP = 1/Rp1 + 1/Rp2

Una vez que hemos calculado las resistencias totales en serie y en paralelo, simplemente sumamos las dos para obtener la resistencia total del circuito mito:

RTotal = RTS + RTP

¡Y eso es todo! Ahora conoces la fórmula para calcular la resistencia total de un circuito mito. Recuerda seguir los pasos mencionados y realizar los cálculos adecuados para obtener el resultado correcto. Este conocimiento te será útil en numerosas aplicaciones prácticas relacionadas con la electrónica y la electricidad.

Qué valores se necesitan para realizar el cálculo de la resistencia total

En la calculadora de resistencia total para circuitos mitos, necesitamos tener claros algunos valores clave para poder realizar el cálculo de manera precisa. Estos valores incluyen la resistencia de cada componente individual en el circuito, así como las coneiones entre ellos.

Para empezar, debemos conocer los valores de resistencia de cada resistor presente en el circuito. Esto se denota comúnmente con la letra "R" seguida de un número subíndice que identifica cada resistor de manera única. Por ejemplo, R1, R2, R3, etc.

Además, también es importante determinar cómo están conectados estos resistores entre sí. Hay dos configuraciones comunes: paralelo y en serie.

Configuración en serie

En una coneión en serie, los resistores están conectados uno después del otro, de manera que la corriente pasa a través de cada uno de ellos en orden. Para calcular la resistencia total en una configuración en serie, simplemente sumamos los valores de las resistencias individuales. Es decir:

R_total = R1 + R2 + R3 + ...

Configuración en paralelo

En cambio, en una configuración en paralelo, los resistores están conectados de manera que la corriente se divide entre ellos. En este caso, el cálculo de la resistencia total es un poco más complejo. La fórmula general para calcular la resistencia total en una configuración en paralelo es:

1/R_total = 1/R1 + 1/R2 + 1/R3 + ...

Una vez que hayamos determinado si los resistores están en serie o en paralelo, podemos usar la fórmula correspondiente para calcular la resistencia total del circuito mito.

Primer paso: identificar el tipo de coneión

Para iniciar el cálculo de la resistencia total, debemos analizar detenidamente el circuito y determinar si los resistores están conectados en serie, en paralelo o ambos. En algunos casos, puede haber combinaciones de ambas configuraciones, lo que se conoce como un circuito mito.

Una buena estrategia para identificar el tipo de coneión es seguir el flujo de la corriente a través de los resistores. Si la corriente fluye continuamente de un resistor al siguiente sin ninguna ramificación, entonces los resistores están conectados en serie. Por otro lado, si la corriente se divide en varias rutas diferentes y luego se une nuevamente después de pasar por los resistores, esto indica una coneión en paralelo.

Es importante recordar que si tenemos una combinación de resistores en serie y en paralelo, primero debemos calcular la resistencia equivalente de las coneiones en serie y paralelo por separado antes de obtener la resistencia total del circuito mito.

Conociendo el tipo de coneión de los resistores, estamos listos para realizar el cálculo de la resistencia total del circuito mito. Recuerda tener en cuenta las fórmulas mencionadas anteriormente según sea necesario.

Conocer las resistencias individuales de los componentes y el tipo de coneión entre ellos son los valores clave necesarios para calcular la resistencia total de un circuito mito. Con esta información, podrás realizar tus propios cálculos y obtener los resultados deseados.

Cómo se calcula la resistencia total si hay resistencias en serie

Si tienes un circuito en el que las resistencias están conectadas en serie, calcular la resistencia total es muy sencillo. En este tipo de coneión, las resistencias se colocan una después de la otra, lo que significa que la corriente pasa a través de todas ellas en el mismo sentido.

Para calcular la resistencia total en un circuito en serie, simplemente necesitas sumar los valores de resistencia de todas las resistencias. Es decir, si tienes tres resistencias con valores de 10 ohmios, 20 ohmios y 30 ohmios respectivamente, la resistencia total sería la suma de estos valores: 10 + 20 + 30 = 60 ohmios.

Rt = R1 + R2 + R3 + ... + Rn

Donde Rt es la resistencia total y R1, R2, R3, ..., Rn son los valores de resistencia de cada resistencia individual.

También es importante recordar que la resistencia total en una coneión en serie siempre será mayor que el valor de resistencia más grande presente en el circuito. Esto se debe a que la resistencia total es la suma de todas las resistencias individuales.

Espero que este primer paso te haya ayudado a comprender cómo calcular la resistencia total en un circuito cuando las resistencias están conectadas en serie. Ahora, sigamos adelante y veamos cómo se calcula la resistencia total en un circuito cuando las resistencias están conectadas en paralelo.

Cómo se calcula la resistencia total si hay resistencias en paralelo

Al hablar de circuitos mitos, es común encontrarse con resistencias en paralelo. Calcular la resistencia total en este tipo de configuración puede parecer complicado al principio, pero en realidad es bastante sencillo.

Para calcular la resistencia total de un circuito mito con resistencias en paralelo, debemos recordar que cuando las resistencias están conectadas en paralelo, la resistencia total es igual al inverso de la suma de los inversos de cada una de las resistencias individuales.

```
R_total = 1 / (1/R1 + 1/R2 + ... + 1/Rn)
```

Donde R_total es la resistencia total del circuito y R1, R2, ... Rn son las resistencias individuales en paralelo.

Veamos un ejemplo para ilustrar el cálculo de resistencia total. Imaginemos un circuito mito con dos resistencias en paralelo: R1 = 10 ohm y R2 = 20 ohm.

Aplicamos la fórmula:

```
R_total = 1 / (1/10 + 1/20)
= 1 / (0.1 + 0.05)
= 1 / 0.15
= 6.67 ohm
```

Por lo tanto, la resistencia total del circuito mito con las resistencias R1 = 10 ohm y R2 = 20 ohm es de 6.67 ohm.

Es importante destacar que este método se aplica únicamente cuando las resistencias se encuentran en paralelo. Si hay resistencias en serie en el circuito mito, entonces debemos utilizar otro método para calcular la resistencia total.

El cálculo de la resistencia total en un circuito mito con resistencias en paralelo puede resolverse utilizando la fórmula de inverso de sumas. Haciendo uso de este método, podremos obtener fácilmente el valor de la resistencia total del circuito.

Qué sucede si hay resistencias mitas en el circuito

En el mundo de la electrónica, los circuitos mitos son etremadamente comunes. Estos circuitos combinan tanto resistencias en serie como en paralelo para crear configuraciones mucho más complejas y versátiles. Pero, ¿qué sucede eactamente cuando hay resistencias mitas en un circuito?

La respuesta es bastante simple: la resistencia total del circuito se calcula de manera diferente. En lugar de simplemente sumar o promediar las resistencias como lo haríamos en un circuito con resistencias en serie o en paralelo, cuando hay resistencias mitas involucradas, debemos realizar algunos cálculos adicionales.

Para comenzar, es importante comprender qué significa tener resistencias en serie y en paralelo. Una resistencia en serie es aquella en la que las resistencias están conectadas una después de la otra, de modo que la corriente fluye a través de cada una de ellas en orden. Por otro lado, una resistencia en paralelo es aquella en la que las resistencias están conectadas de manera que la corriente se divide entre ellas.

Ahora, cuando tenemos un circuito mito con resistencias en serie y en paralelo, debemos descomponer el circuito en diferentes partes y calcular la resistencia total de cada parte por separado. Luego, podemos combinar estas resistencias totales para obtener la resistencia total del circuito mito.

Cómo calcular la resistencia total de un circuito mito

Vamos a ver un ejemplo para entender mejor cómo se realiza este cálculo. Supongamos que tenemos un circuito que consta de dos resistencias en serie, seguidas de dos resistencias en paralelo. Para calcular la resistencia total de este circuito, sigamos estos pasos:

1. Calcula la resistencia total de las resistencias en serie. Esto se hace simplemente sumando las resistencias individuales:
   Rserie = R1 + R2
2. Calcula la resistencia total de las resistencias en paralelo. Esto es un poco más complicado, ya que debemos utilizar la fórmula para calcular la resistencia equivalente de resistencias en paralelo:
   1/Requivalente = 1/R3 + 1/R4
3. Combina las resistencias totales calculadas en los pasos anteriores para obtener la resistencia total del circuito mito:
   Rtotal = Rserie + Requivalente

¡Y eso es todo! Siguiendo estos simples pasos, podemos calcular la resistencia total de un circuito mito sin problemas. Recuerda que siempre es importante tener en cuenta la unidad de medida utilizada para las resistencias (generalmente ohmios) y asegurarse de realizar correctamente los cálculos.

Cuando hay resistencias mitas en un circuito, el cálculo de la resistencia total se vuelve un poco más complicado. Debemos descomponer el circuito en diferentes partes, calcular la resistencia total de cada parte y luego combinar estas resistencias totales para obtener la resistencia total del circuito mito. Sin embargo, con algunos cálculos adicionales y una comprensión clara de las resistencias en serie y en paralelo, este proceso se puede realizar fácilmente.

Es posible aplicar la ley de Ohm para calcular la resistencia total en un circuito mito

Cuando te encuentras con un circuito mito, puede resultar abrumador calcular la resistencia total del mismo. Sin embargo, eiste una herramienta muy útil que nos permite resolver este problema de manera fácil y rápida: la ley de Ohm.

La ley de Ohm establece que la corriente que fluye a través de un conductor es directamente proporcional a la diferencia de potencial aplicada e inversamente proporcional a la resistencia del conductor. Esto puede epresarse mediante la fórmula:

I = V / R

Donde "I" representa la corriente en amperios (A), "V" es la diferencia de potencial en voltios (V) y "R" es la resistencia en ohmios (Ω).

¿Qué es un circuito mito?

Antes de adentrarnos en cómo aplicar la ley de Ohm en un circuito mito, es importante comprender qué es eactamente un circuito mito. Un circuito mito es aquel que combina elementos en serie y en paralelo. En otras palabras, encontraremos tanto resistencias conectadas en serie como en paralelo dentro del mismo circuito.

Las resistencias en serie se conectan una tras otra, de modo que la corriente pasa a través de cada una de ellas de manera secuencial. En cambio, las resistencias en paralelo se conectan de tal forma que la corriente se divide entre ellas, pasando a través de cada una por separado.

Paso 1: Identificar las resistencias en serie

Para empezar a calcular la resistencia total de un circuito mito, es necesario identificar las resistencias que están conectadas en serie. Estas resistencias se sumarán para obtener la resistencia equivalente del conjunto.

1. Identifica los elementos en serie en el circuito mito.
2. Suma todas las resistencias en serie.

Paso 2: Identificar las resistencias en paralelo

A continuación, debes buscar las resistencias que están conectadas en paralelo dentro del circuito. Estas resistencias se calcularán de manera distinta a las resistencias en serie. Para obtener la resistencia equivalente de un conjunto de resistencias en paralelo, utiliza la siguiente fórmula:

1 / R_total = 1 / R1 + 1 / R2 + 1 / R3 + ...

Donde "R_total" es la resistencia total y "R1, R2, R3, ..." son las resistencias en paralelo.

• Identifica los elementos en paralelo en el circuito mito.
• Utiliza la fórmula mencionada para calcular la resistencia total de las resistencias en paralelo.

Paso 3: Calcular la resistencia total

Finalmente, para obtener la resistencia total del circuito mito, debes sumar la resistencia obtenida en el paso 1 (resistencias en serie) con la resistencia obtenida en el paso 2 (resistencias en paralelo).

R_total = R_serie + R_paralelo

Una vez que hayas calculado la resistencia total, tendrás una idea clara de cómo fluye la corriente en el circuito mito y podrás utilizar esta información para otros cálculos relacionados con el sistema eléctrico.

Cabe mencionar que la ley de Ohm es una herramienta fundamental para el análisis de circuitos eléctricos. Sin embargo, hay situaciones más complejas en las que puede ser necesario aplicar leyes adicionales, como las leyes de Kirchhoff, para resolver problemas específicos.

Ahora que conoces el proceso para calcular la resistencia total en un circuito mito, ¡puedes enfrentar cualquier desafío eléctrico con confianza!

Eisten otras leyes o fórmulas útiles para el cálculo de la resistencia total en un circuito mito

Además de la ley de Ohm, que nos permite calcular fácilmente la resistencia total en un circuito serie o paralelo, eisten otras leyes y fórmulas útiles cuando se trata de calcular la resistencia total en un circuito mito.

Ley de Kirchhoff

La ley de Kirchhoff, también conocida como la ley de corrientes de Kirchhoff o la primera ley de Kirchhoff, establece que la suma algebraica de las corrientes que entran y salen de un nodo en un circuito es igual a cero. Es decir:

I1 + I2 + I3 + ... + In = 0

Esta ley nos permite determinar las corrientes que fluyen en cada rama de un circuito mito, lo que es útil para el cálculo de la resistencia total.

Regla de divisor de corriente

La regla del divisor de corriente nos permite calcular la corriente que fluye a través de una rama específica de un circuito mito. Esta regla se basa en la proporcionalidad de las resistencias en serie y nos ayuda a determinar cómo se distribuye la corriente en un circuito.

La fórmula para calcular la corriente en una rama específica utilizando la regla del divisor de corriente es:

I = (V / R) * R

Donde I es la corriente en la rama específica, V es la tensión total del circuito, R es la resistencia en serie a la que queremos calcular la corriente y R es la suma de las resistencias en paralelo a R.

Ley de Ohm generalizada

La ley de Ohm generalizada nos permite calcular la resistencia total en un circuito mito cuando tenemos resistencias tanto en serie como en paralelo. Esta ley se basa en la inversión de la fórmula original de la ley de Ohm y nos permite despejar la resistencia total.

La fórmula para calcular la resistencia total utilizando la ley de Ohm generalizada es:

Rtotal = 1 / (1/R1 + 1/R2 + ... + 1/Rn)

Donde R_total es la resistencia total en el circuito mito y R₁, R₂, ..., R_n son las resistencias individuales en serie o paralelo.

Aplicación de las leyes y fórmulas en un circuito mito

Al combinar todas estas leyes y fórmulas, podemos calcular fácilmente la resistencia total en un circuito mito. Primero, identificamos las ramas en paralelo y sumamos las resistencias en cada rama para obtener una resistencia equivalente. Luego, utilizamos la regla del divisor de corriente para calcular la corriente en cada rama específica. Finalmente, aplicamos la ley de Ohm generalizada para obtener la resistencia total del circuito mito.

Con estas herramientas y conocimientos, ¡ya no tienes que temerle a los circuitos mitos! Sigue practicando y calculando la resistencia total en diferentes configuraciones de circuitos mitos para fortalecer tu comprensión y habilidades en el campo de la electricidad.

Hay alguna manera de simplificar el cálculo de la resistencia total en un circuito mito

El cálculo de la resistencia total en un circuito mito puede parecer complicado a primera vista, pero en realidad hay una manera fácil de simplificarlo. Para entender cómo hacerlo, primero debemos comprender qué es un circuito mito.

Un circuito mito: una combinación de circuitos en serie y en paralelo

Un circuito mito es una combinación de circuitos en serie y circuitos en paralelo. En un circuito serie, los componentes están conectados uno después del otro, mientras que en un circuito en paralelo, los componentes están conectados en diferentes caminos para que la corriente se divida entre ellos.

En un circuito mito, hay secciones que están conectadas de forma serie y otras de forma paralela. Esto significa que las resistencias también se combinan de estas dos formas diferentes.

Cómo calcular la resistencia total en un circuito mito

Para calcular la resistencia total en un circuito mito, debemos seguir algunos pasos sencillos. Aquí hay un ejemplo para que lo comprendas mejor:

1. 1. Identifica las resistencias en cada sección del circuito.

Lo primero que debes hacer es identificar todas las resistencias que hay en cada sección del circuito mito. Puedes encontrar estas resistencias en los diagramas o esquemas del circuito.

2. 2. Calcula las resistencias en cada sección del circuito.

Luego, calcula la resistencia en cada sección del circuito. Para las secciones en serie, simplemente suma todas las resistencias. Para las secciones en paralelo, utiliza la fórmula de la resistencia total en paralelo: 1/RT = 1/R1 + 1/R2 + ... + 1/Rn, donde RT es la resistencia total y R1, R2, ..., Rn son las resistencias individuales.

3. 3. Calcula la resistencia total del circuito.

Finalmente, calcula la resistencia total del circuito mito sumando las resistencias totales de cada sección. Si hay más de una sección en paralelo, simplemente sumas estas resistencias totales. Si hay secciones en serie, puedes usar la fórmula de la resistencia total en serie: RT = R1 + R2 + ... + Rn, donde RT es la resistencia total y R1, R2, ..., Rn son las resistencias totales de cada sección.

Ahora que conoces estos pasos, puedes calcular fácilmente la resistencia total en un circuito mito. Recuerda que practicar con diferentes ejemplos te ayudará a comprender mejor este concepto y ganar confianza en tus habilidades para resolver problemas relacionados con circuitos mitos.

Preguntas frecuentes (FAQ)

1. ¿Qué es un circuito mito?

Un circuito mito es aquel que contiene tanto componentes en serie como en paralelo, lo que permite combinar las ventajas de ambos tipos de coneiones.

2. ¿Cómo se calcula la resistencia total de un circuito mito?

Para calcular la resistencia total de un circuito mito, debes sumar las resistencias en paralelo y luego sumar esa resistencia resultante con las resistencias en serie

.

3. ¿Cuál es la fórmula para calcular la resistencia total en paralelo?

La fórmula para calcular la resistencia total en paralelo es: 1/Rtotal = 1/R1 + 1/R2 + ... + 1/Rn

4. ¿Cuál es la fórmula para calcular la resistencia total en serie?

La fórmula para calcular la resistencia total en serie es: Rtotal = R1 + R2 + ... + Rn

5. ¿Cuál es la importancia de conocer la resistencia total de un circuito mito?

Conocer la resistencia total de un circuito mito es importante para poder determinar la corriente y el voltaje en el circuito, lo cual es fundamental para el diseño y funcionamiento adecuado de cualquier sistema eléctrico.