Aprende cómo representar una fracción en la recta numérica de manera fácil y efectiva

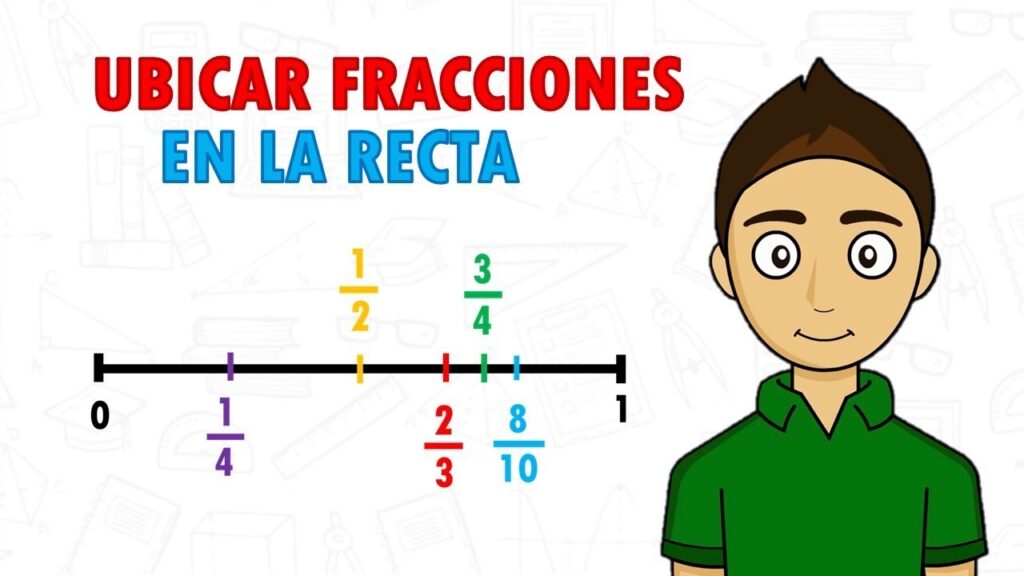
La recta numérica es una herramienta muy útil para representar y visualizar los números. Nos permite ver su posición relativa y realizar operaciones matemáticas de manera más sencilla. Pero, ¿qué pasa cuando queremos representar fracciones en la recta numérica? En este artículo aprenderemos cómo hacerlo de manera fácil y efectiva.

En el siguiente artículo te mostraremos paso a paso cómo representar una fracción en la recta numérica. Eplicaremos cómo dividir un segmento de la recta en partes iguales según el denominador de la fracción y cómo ubicar el punto correspondiente a la fracción en la recta. Además, te daremos algunos ejemplos prácticos para que puedas practicar por ti mismo.

Cómo representar una fracción en la recta numérica paso a paso

La representación de una fracción en la recta numérica es un concepto fundamental en matemáticas. Es una herramienta que nos permite visualizar la posición de una fracción en relación a otros números y facilita la comprensión de las relaciones de magnitud entre ellas.

Para representar una fracción en la recta numérica, sigue estos pasos sencillos:

Paso 1: Identifica el denominador

El denominador de una fracción indica en cuántas partes iguales se divide la unidad. Por ejemplo, si tenemos la fracción 1/4, significa que la unidad se divide en cuatro partes iguales.

Paso 2: Marca el punto de inicio

En la recta numérica, el punto de inicio siempre será el cero. Marca este punto con una pequeña línea vertical o un punto para representar el número cero.

Paso 3: Divide el intervalo entre el cero y la unidad

Considerando el denominador de la fracción, divide el intervalo entre el cero y la unidad en igual cantidad de partes. Si tenemos la fracción 1/4, dividiremos este intervalo en cuatro partes.

Paso 4: Ubica la fracción en la recta numérica

Ahora, toma el numerador de la fracción y ubica tu punto en el intervalo correspondiente. Siguiendo el ejemplo anterior, si tenemos la fracción 1/4, el numerador es 1, por lo tanto, ubicaremos nuestro punto en la primera parte del intervalo.

Paso 5: Finaliza la representación

Por último, puedes agregar una línea horizontal o una flecha desde el punto que representa la fracción hasta la marca del numerador. Esta línea o flecha ayudará a visualizar mejor la posición de la fracción en la recta numérica.

Ahora que conoces estos pasos sencillos, podrás representar cualquier fracción en la recta numérica de manera fácil y efectiva. Recuerda practicar con distintas fracciones para fortalecer tu comprensión y habilidad en este concepto matemático.

Cuáles son las partes de una fracción y cómo se relacionan con la recta numérica

Para representar una fracción en la recta numérica de manera fácil y efectiva, es importante comprender las partes fundamentales de una fracción y cómo se relacionan con esta herramienta visual.

Una fracción está compuesta por dos elementos: el numerador y el denominador. El numerador representa la cantidad de partes que estamos considerando, mientras que el denominador indica el número total de partes en la unidad o conjunto.

Por ejemplo, si tenemos la fracción 3/4, el numerador es 3, lo que significa que estamos considerando 3 partes de un todo, y el denominador es 4, lo que nos indica que el todo está dividido en 4 partes iguales.

La recta numérica es una línea donde los números están distribuidos ordenadamente. Al representar una fracción en la recta numérica, vamos a utilizar puntos o segmentos de línea para indicar su ubicación eacta.

Cómo representar una fracción propia en la recta numérica

Una fracción propia es cuando el numerador es menor que el denominador, por ejemplo, 2/5. Para representarla en la recta numérica, vamos a seguir los siguientes pasos:

1. Dibujamos una línea recta y marcamos los etremos con los números correspondientes al denominador. En este caso, marcaríamos el 0 y el 5.
2. Dividimos la línea en los segmentos correspondientes al denominador. En este caso, dividimos la línea en 5 segmentos iguales.
3. A partir del segmento marcado como cero, contamos hacia la derecha la cantidad de segmentos indicada por el numerador. En este caso, contamos 2 segmentos hacia la derecha.
4. En el segundo segmento contado, colocamos un punto o marcamos ese punto en la recta numérica. Ese punto representa nuestra fracción 2/5 en la recta numérica.

De esta manera, al representar una fracción propia en la recta numérica siguiendo estos pasos, podemos visualizar fácilmente la posición relativa de la fracción con respecto a otros números y fracciones.

Cómo representar una fracción impropia o mayor que 1 en la recta numérica

Una fracción impropia es cuando el numerador es igual o mayor que el denominador, por ejemplo, 7/4. Si queremos representarla en la recta numérica, debemos seguir los siguientes pasos:

1. Dibujamos una línea recta y marcamos los etremos con los números correspondientes al denominador. En este caso, marcaríamos el 0 y el 4.
2. Dividimos la línea en los segmentos correspondientes al denominador. En este caso, dividimos la línea en 4 segmentos iguales.
3. A partir del segmento marcado como cero, contamos hacia la derecha la cantidad de segmentos indicada por el numerador. En este caso, contamos 7 segmentos hacia la derecha.
4. En el séptimo segmento contado, colocamos un punto o marcamos ese punto en la recta numérica. Ese punto representa nuestra fracción 7/4 en la recta numérica.

Es importante tener en cuenta que al representar una fracción impropia en la recta numérica, el punto estará ubicado más allá del número 1, lo que indica que la fracción es mayor que 1.

Representar una fracción en la recta numérica no solo nos ayuda a visualizar mejor su valor y ubicación, sino también a comprender mejor las relaciones de orden entre los números y las fracciones. Además, esta representación gráfica puede ser útil en diversas situaciones, como la comparación de fracciones o la identificación de fracciones equivalentes en un conteto visualmente intuitivo y claro.

Cuál es el rango de valores que se pueden representar en la recta numérica usando fracciones

La recta numérica es una herramienta muy útil para representar y visualizar los números de manera ordenada. En ella, se pueden ubicar tanto números enteros como fracciones, permitiéndonos comprender mejor la relación entre ellos.

Cuando hablamos de representar una fracción en la recta numérica, nos referimos a posicionarla de forma adecuada en relación a los demás números. Para ello, es importante entender el rango de valores que se pueden representar utilizando fracciones en esta herramienta.

En general, cualquier fracción puede ser representada en la recta numérica, ya sea positiva o negativa. Sin embargo, es importante destacar que eisten ciertas limitaciones en cuanto al rango de valores que pueden ser epresados de manera efectiva.

Por ejemplo, si consideramos fracciones con denominador 2, como 1/2, 3/2, -1/2, etc., podemos representarlas en la recta numérica sin problemas, ya que su posición será clara y se pueden ubicar perfectamente entre los números enteros.

Por otro lado, cuando trabajamos con fracciones cuyos denominadores son múltiplos de 2, como 1/4, 3/8, -5/6, etc., también podemos representarlas en la recta numérica con facilidad. La única diferencia es que al aumentar el denominador, la distancia entre las marcas de la recta numérica se reduce, por lo que debemos tener en cuenta este detalle al realizar la representación.

Además, es importante mencionar que todas las fracciones que se encuentran entre dos números enteros consecutivos también pueden ser representadas en la recta numérica. En este caso, la posición de la fracción dependerá de su numerador y denominador, así como de la escala utilizada para la representación.

El rango de valores que se pueden representar en la recta numérica utilizando fracciones es muy amplio. Desde las fracciones simples con denominador 2 hasta aquellas con denominadores más grandes, todas pueden ser ubicadas de manera efectiva en esta herramienta. La clave está en comprender la relación entre los números enteros y las fracciones, así como en utilizar una escala apropiada para lograr una representación clara y precisa.

Cuál es la importancia de representar las fracciones en la recta numérica

La representación de fracciones en la recta numérica es una herramienta fundamental en el aprendizaje de las matemáticas. Esta representación visual permite a los estudiantes comprender y visualizar de manera clara la magnitud de una fracción en relación con otros números y fracciones. La recta numérica proporciona un marco de referencia que facilita la comprensión de conceptos como la equivalencia entre fracciones, la comparación de fracciones y la ubicación de fracciones en relación con números enteros.

Al representar las fracciones en la recta numérica, los estudiantes pueden observar cómo se divide una unidad en partes iguales y cómo diferentes fracciones representan diferentes porciones de esa unidad. Esto les ayuda a conceptualizar las fracciones como puntos en la recta numérica y a relacionarlas con su valor numérico. Al tener una representación visual, los estudiantes pueden realizar comparaciones más precisas entre diferentes fracciones y comprender mejor las relaciones de orden entre ellas.

Además de ayudar en la comprensión de las fracciones, la representación en la recta numérica también facilita la resolución de problemas matemáticos que involucran operaciones con fracciones. Los estudiantes pueden utilizar la recta numérica para sumar, restar, multiplicar y dividir fracciones, siguiendo los pasos adecuados en la dirección correcta. Esto les brinda una estrategia visual que les permite entender el proceso de resolución y verificar sus respuestas de manera intuitiva.

Beneficios de representar las fracciones en la recta numérica

• Facilita la comprensión de conceptos matemáticos relacionados con las fracciones.
• Ayuda a visualizar la magnitud de una fracción en relación con otros números y fracciones.
• Promueve la comprensión de la equivalencia entre fracciones.
• Permite comparar y ordenar fracciones de manera más precisa.
• Proporciona una estrategia visual para resolver operaciones con fracciones.
• Mejora la habilidad de visualización y razonamiento matemático.

Representar las fracciones en la recta numérica es una herramienta valiosa que ayuda a los estudiantes a comprender mejor el mundo de las fracciones, sus relaciones y operaciones. Es una forma efectiva de promover la comprensión conceptual y el pensamiento matemático, permitiendo a los estudiantes desarrollar habilidades fundamentales para resolver problemas y aplicar conceptos matemáticos en su vida diaria.

Cómo identificar la ubicación eacta de una fracción en la recta numérica

Representar una fracción en la recta numérica es una habilidad importante que nos permite visualizar y comprender mejor el valor de una fracción. Al colocar una fracción en la recta numérica, podemos determinar fácilmente su ubicación eacta y compararla con otras fracciones o números enteros.

Para representar una fracción en la recta numérica, necesitamos tener en cuenta algunos pasos sencillos pero fundamentales. Primero, identificamos el denominador de la fracción, que indica en cuántas partes iguales se divide la unidad. Luego, dividimos la recta numérica en el número correspondiente de partes iguales.

A continuación, verificamos el numerador de la fracción, que nos dice cuántas partes iguales de la unidad debemos contar desde el cero. A medida que contamos las partes indicadas por el numerador, marcamos cada punto respectivo en la recta numérica. Finalmente, trazamos una línea recta desde el cero hasta el punto marcado y ¡listo! Hemos representado eitosamente nuestra fracción en la recta numérica.

Ejemplo:

Supongamos que queremos representar la fracción 3/4 en la recta numérica. Comenzamos dividiendo la recta en cuatro partes iguales, ya que el denominador es 4. Luego, contamos tres partes, ya que el numerador es 3. Marcamos ese punto en la recta y trazamos una línea recta desde el cero hasta ese punto. Ahora tenemos la representación visual de la fracción 3/4 en la recta numérica.

Es importante tener en cuenta que la recta numérica nos permite no solo representar fracciones propias, sino también fracciones impropias y números mitos. Para fracciones impropias, el numerador será mayor que el denominador, por lo que se etenderá más allá de la unidad en la recta numérica.

En el caso de los números mitos, primero representamos la parte entera (número antes de la fracción) en la recta y luego seguimos los mismos pasos para representar la fracción en su ubicación correspondiente después de la parte entera. Esto nos brinda una representación visual clara y precisa de los números mitos en la recta numérica.

Representar una fracción en la recta numérica es un proceso sencillo pero efectivo que nos ayuda a entender y visualizar mejor el valor de las fracciones. Al seguir pasos como identificar el denominador, dividir la recta en partes iguales, contar el numerador y marcar los puntos respectivos, podemos representar cualquier fracción en la recta numérica y compararla con facilidad con otros números.

Qué estrategias puedes utilizar para representar fracciones mitas en la recta numérica

Representar fracciones mitas en la recta numérica puede parecer un desafío, pero eisten varias estrategias efectivas que puedes utilizar para facilitar este proceso. En este artículo, te proporcionaremos algunas recomendaciones prácticas que te ayudarán a visualizar y representar fracciones mitas de manera fácil y precisa.

1. Convierte la fracción mita en una fracción impropia

Antes de comenzar a representar una fracción mita en la recta numérica, es útil convertirla en una fracción impropia. Para hacer esto, multiplica el denominador por el número entero y suma el numerador. El resultado será el numerador de la nueva fracción impropia, y el denominador permanecerá igual.

Ejemplo:
Fracción mita: 2 3/4
Fracción impropia: (2 * 4) + 3 / 4 = 11/4

2. Determina una escala adecuada para la recta numérica

Una vez que hayas convertido la fracción mita en una fracción impropia, debes determinar una escala adecuada para la recta numérica en la que vas a representarla. La escala debe considerar tanto el numerador como el denominador de la fracción impropia, asegurando que haya suficiente espacio para representar todos los valores.

3. Divide la recta numérica en partes iguales según el denominador

Una vez que hayas establecido la escala de la recta numérica, divídela en partes iguales según el denominador de la fracción impropia. Por ejemplo, si el denominador es 4, divide la recta en 4 partes iguales.

4. Marca el punto inicial

El siguiente paso consiste en ubicar el punto inicial de la representación de la fracción impropia en la recta numérica. Para esto, debes utilizar el número entero de la fracción mita convertida y marcarlo en la escala establecida previamente.

5. Determina la posición del resto de la fracción impropia

A continuación, debes determinar la posición del numerador en relación con el denominador en la recta numérica. Si el numerador es menor que el denominador, coloca el punto correspondiente en la parte adecuada de la subdivisión.

6. ¡Listo! Has representado la fracción mita en la recta numérica

Una vez que hayas seguido los pasos anteriores, habrás representado eitosamente la fracción mita en la recta numérica. Recuerda que este método también funciona para representar fracciones propias, simplemente omite el número entero al iniciar el proceso de representación.

Representar fracciones mitas en la recta numérica se puede lograr utilizando estrategias simples pero efectivas. Convirtiendo la fracción mita en una fracción impropia, determinando una escala adecuada, dividiendo la recta numérica en partes iguales, marcando el punto inicial y posicionando el numerador correctamente, podrás visualizar fracciones mitas de manera clara y precisa.

Eisten trucos o tips que puedan facilitar la representación de fracciones en la recta numérica

La representación de fracciones en la recta numérica puede resultar confusa para muchos estudiantes. Sin embargo, eisten algunos trucos y tips que pueden facilitar este proceso y hacerlo mucho más fácil y efectivo.

1. Entender el concepto de fracción

Antes de adentrarnos en la representación de fracciones en la recta numérica, es importante entender el concepto mismo de fracción. Una fracción se compone de dos partes: el numerador y el denominador. El numerador representa la cantidad de partes que tenemos, mientras que el denominador indica en cuántas partes se divide el todo. Por ejemplo, en la fracción 3/4, el numerador es 3 y el denominador es 4.

2. Dividir la recta numérica en partes iguales

Una vez que tenemos claro el concepto de fracción, podemos proceder a representarla en la recta numérica. Para ello, primero debemos dividir la recta en partes iguales según el denominador de la fracción. Por ejemplo, si queremos representar la fracción 3/4, dividimos la recta en 4 partes iguales.

3. Marcar el punto correspondiente al numerador

El siguiente paso es marcar el punto correspondiente al numerador de la fracción en la recta numérica. En nuestro ejemplo, como el numerador es 3, contamos 3 partes desde el inicio de la recta y marcamos ese punto.

4. Conectar los puntos

Una vez que hemos marcado el punto correspondiente al numerador, podemos trazar una línea que conecte ese punto con el origen de la recta numérica. Esta línea representa la fracción y nos ayuda a visualizar su posición en la recta.

5. Reforzar con ejercicios prácticos

La representación de fracciones en la recta numérica es un concepto que se fortalece con práctica. Es recomendable realizar ejercicios prácticos que involucren la representación de diferentes fracciones en la recta numérica. Esto ayudará a reforzar el aprendizaje y mejorar la comprensión del tema.

La representación de fracciones en la recta numérica puede ser más fácil de lo que parece si se siguen algunos trucos y se practica de manera constante. Entender el concepto de fracción, dividir la recta en partes iguales, marcar el punto correspondiente al numerador, conectar los puntos y reforzar con ejercicios prácticos son pasos clave para lograr una representación precisa y efectiva de las fracciones en la recta numérica.

Qué hacer en caso de tener fracciones con denominadores diferentes

Representar una fracción en la recta numérica puede parecer una tarea complicada, especialmente cuando se trata de fracciones con denominadores diferentes. Sin embargo, eisten métodos fáciles y efectivos que te ayudarán a visualizar estas fracciones de manera clara.

Antes de eplorar cómo representar fracciones con denominadores diferentes en la recta numérica, es importante recordar cómo funciona esta herramienta visual. La recta numérica es una línea horizontal donde los números enteros se ubican en puntos específicos. Cada punto en la recta representa un número en el espectro numérico.

1. Identificar las fracciones a representar

Lo primero que debes hacer es identificar las fracciones que deseas representar en la recta numérica. Para este ejemplo, supongamos que tenemos las fracciones 1/4 y 3/5. Estas fracciones tienen denominadores diferentes, lo que complica su representación directa en la recta.

2. Encontrar un monto común para los denominadores

La clave para representar fracciones con denominadores diferentes en la recta numérica es encontrar un monto común para ambos denominadores. Esto permitirá crear intervalos uniformes que faciliten la ubicación de las fracciones.

En nuestro ejemplo, podemos encontrar un monto común multiplicando los denominadores entre sí. Multiplicando 4 por 5 obtenemos 20, lo cual sería nuestro nuevo denominador común.

3. Dividir la recta numérica en segmentos iguales

Una vez que tenemos el denominador común, debemos dividir la recta numérica en segmentos iguales que representen este valor. En nuestro caso, al tener un denominador común de 20, dividiremos la recta en 20 segmentos iguales.

Recuerda etiquetar los puntos de división con los números correspondientes. Al estar trabajando con el ejemplo de las fracciones 1/4 y 3/5, etiquetaríamos los puntos de división de la recta desde 0 hasta 20.

4. Ubicar las fracciones en la recta numérica

Ahora viene la parte donde ubicamos nuestras fracciones en los segmentos de la recta numérica. Comenzaremos ubicando la fracción 1/4. Para hacerlo, tomamos el numerador (1) y lo ubicamos en el segmento correspondiente, es decir, el segmento número 5 (correspondiente al denominador 20).

A continuación, ubicamos la fracción 3/5 en la recta numérica. Tomamos el numerador (3) y lo ubicamos en el segmento correspondiente, es decir, el segmento número 12 (también correspondiente al denominador 20).

5. Analizar la representación de las fracciones

Una vez que hemos ubicado ambas fracciones en la recta numérica, es importante analizar su representación visual. Observamos que la fracción 1/4 se encuentra hacia el inicio de la recta, mientras que la fracción 3/5 se encuentra más cerca del final.

Esto nos indica que la fracción 1/4 es menor en valor que la fracción 3/5. La representación en la recta numérica nos ayuda a visualizar esta relación de manera más clara.

Representar fracciones con denominadores diferentes en la recta numérica puede ser una tarea sencilla si seguimos los pasos adecuados. Al identificar las fracciones a representar, encontrar un denominador común, dividir la recta numérica en segmentos iguales y ubicar las fracciones en su posición correspondiente, logramos visualizar de manera efectiva estas fracciones en el conteto de la recta.

Recuerda practicar con distintos ejemplos de fracciones con denominadores diferentes para mejorar tu habilidad de representación visual en la recta numérica. ¡Sigue aprendiendo y dominando este importante concepto matemático!

Es posible representar fracciones negativas en la recta numérica

Representar fracciones en la recta numérica es una forma visual muy útil para entender el valor relativo de las fracciones. A menudo, se enseña cómo representar fracciones positivas en la recta numérica, pero ¿qué pasa con las fracciones negativas?

¡La buena noticia es que también es posible representar fracciones negativas en la recta numérica! Al igual que con las fracciones positivas, utilizaremos la recta numérica como una línea horizontal donde ubicaremos las fracciones según su valor.

Para representar fracciones negativas en la recta numérica, primero debemos recordar que los números negativos se encuentran a la izquierda del cero en la línea numérica. Por lo tanto, colocaremos las fracciones negativas en esa parte de la recta.

Tomemos como ejemplo la fracción -1/2. Para representarla en la recta numérica, comenzaremos colocando un punto en el número -1. Luego, dibujaremos una flecha hacia la izquierda desde ese punto y la etenderemos hasta llegar al número -1/2.

Podemos ver que la fracción -1/2 se sitúa justo a la mitad entre los números enteros -1 y 0 en la recta numérica. Esto significa que tiene un valor menor que -1 pero mayor que -2. Es decir, se encuentra más cerca de cero pero todavía en la parte negativa de la recta.

Ahora que sabemos cómo representar fracciones negativas en la recta numérica, podemos practicar con otros ejemplos y adquirir mayor familiaridad con este concepto.

Cómo utilizar la representación gráfica de fracciones en la recta numérica para compararlas y ordenarlas

La representación gráfica de fracciones en la recta numérica es una herramienta muy útil para comparar y ordenar fracciones. Esta representación nos permite visualizar de manera clara la relación entre diferentes fracciones, facilitando su comprensión y análisis.

Paso 1: Establecer un intervalo en la recta numérica

El primer paso para representar una fracción en la recta numérica es establecer un intervalo adecuado. Este intervalo debe ser lo suficientemente amplio como para incluir todas las fracciones que queremos representar. Por ejemplo, si queremos representar fracciones con denominadores del 2 al 8, podemos establecer el intervalo entre 0 y 1.

Paso 2: Dividir el intervalo en partes iguales

Una vez que tenemos nuestro intervalo definido, debemos dividirlo en partes iguales según el denominador de la fracción que queremos representar. Si queremos representar una fracción con denominador 4, dividiremos el intervalo en 4 partes iguales. Cada una de estas partes representará una unidad fraccionaria.

Paso 3: Ubicar la fracción en la recta numérica

Para ubicar una fracción en la recta numérica, contamos desde el punto inicial del intervalo el número de unidades fraccionarias equivalente al numerador de la fracción. Por ejemplo, si queremos representar la fracción 3/4, contaremos 3 unidades fraccionarias a partir del punto inicial del intervalo.

También es importante tener en cuenta si la fracción es propia o impropia. Si la fracción es propia, es decir, su numerador es menor que su denominador, su ubicación estará entre dos unidades fraccionarias consecutivas. Si la fracción es impropia, su ubicación se encontrará más allá de la última unidad fraccionaria.

Si tenemos varias fracciones para representar, podemos compararlas y ordenarlas fácilmente en la recta numérica. Las fracciones ubicadas más cerca del cero serán las más pequeñas y las ubicadas más alejadas serán las más grandes.

Ejemplo práctico:

Veamos un ejemplo práctico. Supongamos que queremos representar las fracciones 1/2, 1/4, y 3/4 en la recta numérica:

• Para representar 1/2, dividimos el intervalo en 2 partes iguales y contamos una unidad desde el punto inicial del intervalo.
• Para representar 1/4, también dividimos el intervalo en 4 partes iguales y contamos una unidad desde el punto inicial del intervalo.
• Para representar 3/4, dividimos el intervalo en 4 partes iguales y contamos tres unidades desde el punto inicial del intervalo.

Representando estas fracciones en la recta numérica, podemos observar claramente que 1/4 es más pequeña que 1/2, mientras que 3/4 está más cerca de 1 que las otras dos fracciones. Esto nos permite comparar y ordenar las fracciones de manera fácil y efectiva.

La representación gráfica de fracciones en la recta numérica es una herramienta valiosa para comparar y ordenar fracciones. Siguiendo los pasos mencionados anteriormente, podemos representar fracciones de manera precisa y visualizar su relación con otras fracciones. Esto facilita el aprendizaje y la comprensión de las fracciones, especialmente para aquellos estudiantes que son más visuales.

1. ¿Cómo se representa una fracción en la recta numérica?

Para representar una fracción en la recta numérica, dividimos la línea entre 0 y 1 en partes iguales según el denominador de la fracción y marcamos el punto correspondiente al numerador.

2. ¿Cuál es el punto de referencia para representar las fracciones en la recta numérica?

El punto de referencia es el número 1 en la recta numérica. Las fracciones menores a 1 se ubican a la izquierda del número 1, mientras que las fracciones mayores a 1 se ubican a la derecha del número 1.

3. ¿Qué indica la posición de una fracción en la recta numérica?

La posición de una fracción en la recta numérica indica su tamaño o valor relativo respecto a otros números. Cuanto más cerca está de 0, menor es la fracción, y cuanto más cerca está de 1, mayor es la fracción.

4. ¿Cómo se representa una fracción impropia en la recta numérica?

Una fracción impropia se representa ubicando su punto en la recta numérica más allá del número 1. La distancia entre el número 1 y el punto de la fracción impropia dependerá de su numerador.

5. ¿Qué ocurre si la fracción tiene un denominador mayor que el número 10 en la recta numérica?

Si el denominador de una fracción es mayor que el número 10, será más difícil representarla con precisión en la recta numérica. En ese caso, se pueden utilizar marcas adicionales para indicar partes más pequeñas de la unidad.